Question

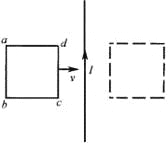
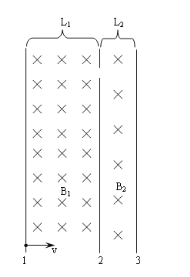
【题目】如图所示，1、2、3为足够长的竖直边界，1和2之间的距离为，2和3之间的距离为，1、2之间和2、3之间均有垂直于纸面向里的匀强磁场，1、2之间的磁场的磁感应强度为，2、3之间的磁场的磁感应强度为，一个质量为m，带电量为+q的粒子以水平初速度v进入磁场。

（1）若初速度，粒子能从3边界飞出磁场，求粒子在两个磁场中做圆周运动的半径各是多少？（最后结果用m、v1、q、B表示）

（2）若粒子刚好不从3边界飞出，求粒子进入磁场时的水平初速度大小；(最后结果用L1、L2、q、B、m表示)

（3）在（2）的情景下，若已知粒子从1边界运动到2边界的时间为，求粒子从1边界进入磁场到从1边界飞出磁场的总时间T总。（最后结果用π、m、q、B表示）

Answer 1

【答案】（1） （2）（3）

【解析】

（1）根据洛伦兹力等于向心力列式求解运动半径；（2）粒子进入磁场时的水平初速度最小时，粒子运动的轨迹在3边界刚好相切，求得粒子在两个磁场中运动的最小半径，结合几何关系求解最小速度；（3）根据求解在两部分磁场中的运动时间。

（1）由 得：

由得：

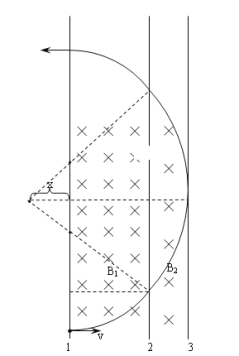
（2）如图所示，粒子运动的轨迹在3边界刚好相切。

由可知：

同理可得：

由几何关系可得：

联解以上四式可得：

（3）设从1边界运动到2边界的圆弧对应的圆心角为θ，则有

由以上三式可得

由几何知识可得：从2边界运动到3边界的圆弧对应的圆心角为

从2边界运动到3边界的时间为

所以总时间T总=