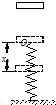题目内容
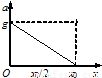
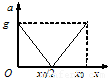
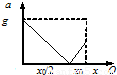
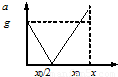
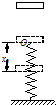 如图所示,下端固定的一根轻弹簧竖直立在水平地面上,弹簧正上方有一物块,从高处自由下落到弹簧上端的O点,开始将弹簧压缩.弹簧被压缩了x0时,物块的速度变为零.从O点开始接触,物块加速度的数值随弹簧O点下降高度x的变化图象是右图中的( )
如图所示,下端固定的一根轻弹簧竖直立在水平地面上,弹簧正上方有一物块,从高处自由下落到弹簧上端的O点,开始将弹簧压缩.弹簧被压缩了x0时,物块的速度变为零.从O点开始接触,物块加速度的数值随弹簧O点下降高度x的变化图象是右图中的( )分析:根据牛顿第二定律求出加速度a与下降高度x的关系式,判断a随x的变化规律.若从弹簧原长位置释放,平衡位置在最终压缩量的一半,现在从某一高度下降,平衡位置不再是压缩量的一半.
解答:解:在平衡位置以上,重力大于弹力,有a=
=g-
,在平衡位置以下,重力小于弹力,有a=
=
-g,知a与x成线性关系.若物体从弹簧原长位置释放,根据对称性,平衡位置在最终压缩量的中点,最低点的加速度等于g,从某一高度释放,要下降得更低,最低点的弹力会更大,根据牛顿第二定律,加速度应大于g.故D正确,A、B、C错误.
故选D.
| mg-kx |
| m |
| kx |
| m |
| kx-mg |
| m |
| kx |
| m |
故选D.
点评:解决本题的关键会根据牛顿第二定律求出加速度的表达式,知道a与x的关系,通过与弹簧原长位置释放进行比较,得出最低点加速度的大小关系.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
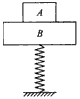
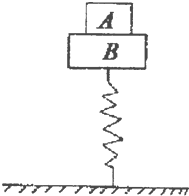 如图所示,下端固定的竖直轻弹簧的上端与质量为3kg的物体B连接,质量为1kg的物体A放在B上,先用力将弹簧压缩后释放,它们向上运动,当A、B分离后A又上升0.2m到达最高点,这时B的运动方向向下且弹簧恰好恢复原长,当A、B分离后A又上升0.2m的过程中弹簧弹力对B的冲量大小(g取10m/s2)
如图所示,下端固定的竖直轻弹簧的上端与质量为3kg的物体B连接,质量为1kg的物体A放在B上,先用力将弹簧压缩后释放,它们向上运动,当A、B分离后A又上升0.2m到达最高点,这时B的运动方向向下且弹簧恰好恢复原长,当A、B分离后A又上升0.2m的过程中弹簧弹力对B的冲量大小(g取10m/s2)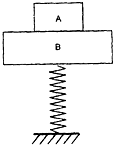 如图所示,下端固定的竖直轻弹簧的上端与质量为5kg物体B连接,质量为0.8kg的A物体放在B上,先用力将弹簧压缩后释放,它们向上运动,当A、B分离后,A又上升0.2m到达最高点,这时B的运动方向向下,且弹簧恰好恢复到原长,则从A、B分离至A达到最高点的过程中(g=lOm/s2)( )
如图所示,下端固定的竖直轻弹簧的上端与质量为5kg物体B连接,质量为0.8kg的A物体放在B上,先用力将弹簧压缩后释放,它们向上运动,当A、B分离后,A又上升0.2m到达最高点,这时B的运动方向向下,且弹簧恰好恢复到原长,则从A、B分离至A达到最高点的过程中(g=lOm/s2)( )