题目内容
(2003?肇庆模拟)根据量子理论,光子具有动量.光子的动量等于光子的能量除以光速,即P=E/c.光照射到物体表面并被反射时,会对物体产生压强,这就是“光压”.光压是光的粒子性的典型表现.光压的产生机理如同气体压强:由大量气体分子与器壁的频繁碰撞产生了持续均匀的压力,器壁在单位面积上受到的压力就是气体的压强.
(1)激光器发出的一束激光的功率为P,光束的横截面积为S.当该激光束垂直照射在物体表面时,试计算单位时间内到达物体表面的光子的总动量.
(2)若该激光束被物体表面完全反射,试求出其在物体表面引起的光压表达式.
(3)设想利用太阳的光压将物体送到太阳系以外的空间去,当然这只须当太阳对物体的光压超过了太阳对物体的引力才行.现如果用一种密度为1.0×103kg/m3的物体做成的平板,它的刚性足够大,则当这种平板厚度较小时,它将能被太阳的光压送出太阳系.试估算这种平板的厚度应小于多少(计算结果保留二位有效数字)?设平板处于地球绕太阳运动的公转轨道上,且平板表面所受的光压处于最大值,不考虑太阳系内各行星对平板的影响.已知地球公转轨道上的太阳常量为1.4×103J/m2?s(即在单位时间内垂直辐射在单位面积上的太阳光能量),地球绕太阳公转的加速度为5.9×10-3m/s2)
(1)激光器发出的一束激光的功率为P,光束的横截面积为S.当该激光束垂直照射在物体表面时,试计算单位时间内到达物体表面的光子的总动量.
(2)若该激光束被物体表面完全反射,试求出其在物体表面引起的光压表达式.
(3)设想利用太阳的光压将物体送到太阳系以外的空间去,当然这只须当太阳对物体的光压超过了太阳对物体的引力才行.现如果用一种密度为1.0×103kg/m3的物体做成的平板,它的刚性足够大,则当这种平板厚度较小时,它将能被太阳的光压送出太阳系.试估算这种平板的厚度应小于多少(计算结果保留二位有效数字)?设平板处于地球绕太阳运动的公转轨道上,且平板表面所受的光压处于最大值,不考虑太阳系内各行星对平板的影响.已知地球公转轨道上的太阳常量为1.4×103J/m2?s(即在单位时间内垂直辐射在单位面积上的太阳光能量),地球绕太阳公转的加速度为5.9×10-3m/s2)
分析:(1)设单位时间内激光器发出的光子数,根据激光器的功率求解
(2)求出光子的动量,由动量定理求出压力,然后求出光压.
(3)利用太阳的光压将平板送到太阳系以外的空间去,必须满足条件:太阳对平板的压力大于太阳对其的引力求解.
(2)求出光子的动量,由动量定理求出压力,然后求出光压.
(3)利用太阳的光压将平板送到太阳系以外的空间去,必须满足条件:太阳对平板的压力大于太阳对其的引力求解.
解答:解:(1)设单位时间内激光器发出的光子数为n,每个光子的能量为E,动量为p,则激光器的功率为
P=nE
所以,单位时间内到达物体表面的光子总动量为:
p总=np=
=
(2)激光束被物体表面完全反射时,其单位时间内的动量改变量为:
△p=2p总=2
根据动量定理,激光束对物体表面的作用力为:
F=2
因此,激光束在物体表面引起的光压为:
p压=2
(3)设平板的质量为m,密度为ρ,厚度为d,面积为s,已知太阳常量为J;地球绕太阳公转的加速度为a.利用太阳的光压将平板送到太阳系以外的空间去,必须满足条件:太阳对平板的压力大于太阳对其的引力.结合(2)的结论,有:
2J
>ma
而平板的质量m=ρds
所以:d<
解以上各式可得:d<1.6×10-6(m)
因此,平板的厚度应小于1.6×10-6(m)
答:(1)单位时间内到达物体表面的光子的总动量是
.
(2)其在物体表面引起的光压表达式是2
.
(3)这种平板的厚度应小于1.6×10-6(m)
P=nE
所以,单位时间内到达物体表面的光子总动量为:
p总=np=
| nE |
| c |
| p |
| c |
(2)激光束被物体表面完全反射时,其单位时间内的动量改变量为:
△p=2p总=2
| p |
| c |
根据动量定理,激光束对物体表面的作用力为:
F=2
| p |
| c |
因此,激光束在物体表面引起的光压为:
p压=2
| p |
| cs |
(3)设平板的质量为m,密度为ρ,厚度为d,面积为s,已知太阳常量为J;地球绕太阳公转的加速度为a.利用太阳的光压将平板送到太阳系以外的空间去,必须满足条件:太阳对平板的压力大于太阳对其的引力.结合(2)的结论,有:
2J
| s |
| c |
而平板的质量m=ρds
所以:d<
| 2J |
| cρa |
解以上各式可得:d<1.6×10-6(m)
因此,平板的厚度应小于1.6×10-6(m)
答:(1)单位时间内到达物体表面的光子的总动量是
| p |
| c |
(2)其在物体表面引起的光压表达式是2
| p |
| cs |
(3)这种平板的厚度应小于1.6×10-6(m)
点评:本题难度并不大,但解题时一定要细心、认真,应用动量定理与牛顿第二定律即可解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2003?肇庆模拟)用如图所示的装置进行以下实验:
(2003?肇庆模拟)用如图所示的装置进行以下实验: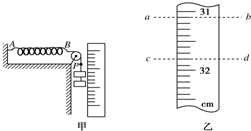 (2003?肇庆模拟)用如图甲所示的装置测定弹簧的劲度系数,被测弹簧一端固定于A点,另一端B用细绳绕过定滑轮挂钩码,旁边竖直固定一最小刻度为mm的刻度尺,当挂两个钩码时,绳上一定点P对应刻度如图乙中ab虚线所示,再增加一个钩码后,P点对应刻度如图乙中cd虚线所示,已知每个钩码质量为50g,重力加速度g=9.8m/s2,则被测弹簧的劲度系数为
(2003?肇庆模拟)用如图甲所示的装置测定弹簧的劲度系数,被测弹簧一端固定于A点,另一端B用细绳绕过定滑轮挂钩码,旁边竖直固定一最小刻度为mm的刻度尺,当挂两个钩码时,绳上一定点P对应刻度如图乙中ab虚线所示,再增加一个钩码后,P点对应刻度如图乙中cd虚线所示,已知每个钩码质量为50g,重力加速度g=9.8m/s2,则被测弹簧的劲度系数为 (2003?肇庆模拟)一个质量m=0.20kg的小球系于轻质弹簧的一端,且套在光滑竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.50m,劲度系数为4.8N/m,如图所示,若小球从图中所示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能Ep弹=0.60J.
(2003?肇庆模拟)一个质量m=0.20kg的小球系于轻质弹簧的一端,且套在光滑竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.50m,劲度系数为4.8N/m,如图所示,若小球从图中所示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能Ep弹=0.60J. (2003?肇庆模拟)在把电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
(2003?肇庆模拟)在把电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: