题目内容
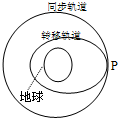（2008?汕头二模）发射通信卫星的常用方法是：先用火箭将卫星送入一个椭圆轨道（转移轨道），如图所示，当卫星到达远地点P时，打开卫星上的发动机，使之进入与地球自转同步的圆形轨道（同步轨道）．设卫星在轨道改变前后的质量不变，那么，卫星在“同步轨道”与在“转移轨道”的远地点相比（ ）分析：当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动
1．若是供大于需 则卫星做逐渐靠近圆心的运动
2．若是供小于需 则卫星做逐渐远离圆心的运动
1．若是供大于需 则卫星做逐渐靠近圆心的运动
2．若是供小于需 则卫星做逐渐远离圆心的运动
解答：解：A、卫星受地球的万有引力就是卫星的合力．
根据牛顿第二定律得：
a=
=
，M为地球质量，r为卫星到地球中心的距离．
所以卫星在“同步轨道”与在“转移轨道”的远地点相比，加速度不变．故A错误．
B、周期是做一个周期性的运动所需要的时间，所以在某一点不好比较周期，故B错误．
C、在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动，要实现这个运动必须万有引力小于卫星所需向心力，所以应给卫星加速，增加所需的向心力．即卫星在“同步轨道”与在“转移轨道”的远地点相比速度变大，故C正确．
D、卫星在“同步轨道”与在“转移轨道”的远地点相比重力势能不变，动能较大，所以机械能较大，故D正确．
故选CD．
根据牛顿第二定律得：
a=
| F |
| m |
| GM |
| r2 |
所以卫星在“同步轨道”与在“转移轨道”的远地点相比，加速度不变．故A错误．
B、周期是做一个周期性的运动所需要的时间，所以在某一点不好比较周期，故B错误．
C、在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动，要实现这个运动必须万有引力小于卫星所需向心力，所以应给卫星加速，增加所需的向心力．即卫星在“同步轨道”与在“转移轨道”的远地点相比速度变大，故C正确．
D、卫星在“同步轨道”与在“转移轨道”的远地点相比重力势能不变，动能较大，所以机械能较大，故D正确．
故选CD．
点评：比较一个物理量，我们应该把这个物理量先用已知的物理量表示出来，再根据表达式进行比较．
卫星变轨也就是近心运动或离心运动，根据提供的万有引力和所需的向心力关系确定．
卫星变轨也就是近心运动或离心运动，根据提供的万有引力和所需的向心力关系确定．
练习册系列答案
应用题作业本系列答案
相关题目
（2008?汕头二模）如图所示，图中MN是由负点电荷产生的电场中的一条电场线．一带电粒子+q飞入电场后，只在电场力作用下沿图中虚线运动，a、b是该曲线上的两点，则下列说法正确的是（ ）
（2008?汕头二模）如图所示，电路中A、B是完全相同的灯泡，L是一带铁芯的线圈，开关S原来闭合，则开关S断开的瞬间（ ）
（2008?汕头二模）如图，质量为M、长度为l的小车静止在光滑的水平面上．质量为m的小物块（可视为质点）放在小车的最左端．现用一水平恒力F作用在小物块上，使物块从静止开始做匀加速直线运动．物块和小车之间的摩擦力为Ff．物块滑到小车的最右端时，小车运动的距离为s．在这个过程中，以下结论正确的是（ ）