题目内容
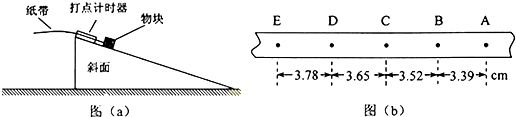
15.在学习了伏安法测电阻之后,某课外活动小组想通过如图1所示的实验电路测定一个阻值约为几十欧的电阻Rx的阻值.图中定值电阻R0=10Ω,R是总阻值为50Ω的滑动变阻器,A1和A2是电流表,电源电动势E=4V,电源内阻忽略不计.(1)该课外活动小组现有四只可供选择的电流表:
A.电流表(0~3mA,内阻为2.0Ω)
B.电流表(0~0.3A,内阻为5.0Ω)
C.电流表(0~3mA,内阻未知)
D.电流表(0~0.6A,内阻未知)
则电流表A1应选B;电流表A2应选D.(填器材前的字母)
(2)在不损坏电表的情况下,将滑动变阻器的滑片从最左端逐渐向右滑动,随着滑动变阻器接入电路中的长度x的变化,电流表A2的示数也随之发生变化,则下列四个选项中能正确反映电流表A2的示数I2随滑动变阻器接入电路中的长度x的变化关系的是图2中的B.
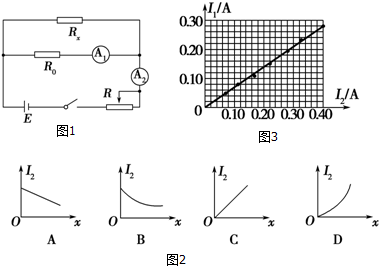
(3)该课外活动小组利用图1所示的电路,通过改变滑动变阻器接入电路中的阻值,得到了若干组电流表A1、A2的示数I1、I2,然后在坐标纸上描点、连线,得到的I1-I2图线如图3所示,由图可知,该待测电阻Rx的阻值为35.0Ω.(结果保留三位有效数字)
分析 (1)根据实验电路图、电压表的改装原理与电流表的量程分析答题;
(2)根据欧姆定律求出图象的函数表达式,然后分析答题;
(3)根据电路图与欧姆定律求出图象的函数表达式,然后根据函数表达式与图示图象求出电阻阻值.
解答 解:(1)由于在该实验电路中没有电压表,所以要将定值电阻R0和电流表改装成电压表使用,因此电流表A1的内阻应已知,如果采用A电流表,则流经该电流表的最大电流约为$\frac{1}{3}$A,超出了该电流表的量程,如果采用B电流表,则流经该电流表的最大电流约为$\frac{4}{15}$A,小于该电流表的量程,所以A1应选用B电流表.
由于电流表A2的内阻不是必须要知道的,其量程要大于电流表A1的量程,所以电流表A2应选择D电流表.
(2)流经电流表A2的电流为电路中的总电流,设滑动变阻器单位长度的电阻为r,则有I2=$\frac{E}{\frac{({R}_{0}+{R}_{1}){R}_{X}}{{R}_{0}+{R}_{1}+{R}_{X}}+{R}_{2}+{r}_{X}}$,又因为R0、Rx、R1、R2等均为定值,令k=$\frac{({R}_{0}+{R}_{1}){R}_{X}}{{R}_{0}+{R}_{1}+{R}_{X}}$+R2,则上式可变为I2=$\frac{E}{k+{r}_{X}}$,由数学关系可知,B正确,故选B.
(3)根据图示电路图,由欧姆定律可知:(R0+R1)I1=Rx(I2-I1),整理可得:$\frac{{R}_{X}}{{R}_{X}+{R}_{0}+{R}_{1}}$=$\frac{{I}_{1}}{{I}_{2}}$,而$\frac{{I}_{1}}{{I}_{2}}$即题图中I1-I2图线的斜率,由图可知,$\frac{{I}_{1}}{{I}_{2}}$=$\frac{7}{10}$,解得:Rx=35.0Ω.
故答案为:(1)B;D;(2)B;(3)35.0.
点评 本题考查了实验器材的选择、实验数据处理,要掌握实验器材的选择原则,分析清楚图示图象、应用欧姆定律求出图象的函数表达式是解题的关键.

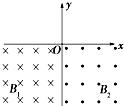 如图所示,在x轴下方的第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,磁感应强度B1=2B2=2B,带电粒子a、b分别从x轴上的P、Q两点(图中没有标出)以垂直于x轴方向的速度同时进入匀强磁场B1、B2中,两粒子恰在第一次通过y轴时发生正碰,碰撞前带电粒子a的速度方向与y轴正方向成60°角,若两带电粒子的比荷分别为k1、k2,进入磁场时的速度大小分别为v1、v2,不计粒子重力和两粒子间相互作用,则下列关系正确的是( )
如图所示,在x轴下方的第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,磁感应强度B1=2B2=2B,带电粒子a、b分别从x轴上的P、Q两点(图中没有标出)以垂直于x轴方向的速度同时进入匀强磁场B1、B2中,两粒子恰在第一次通过y轴时发生正碰,碰撞前带电粒子a的速度方向与y轴正方向成60°角,若两带电粒子的比荷分别为k1、k2,进入磁场时的速度大小分别为v1、v2,不计粒子重力和两粒子间相互作用,则下列关系正确的是( )| A. | k1=2k2 | B. | 2k1=k2 | C. | v1=2v2 | D. | 2v1=v2 |
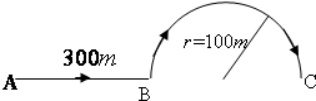
| A. | 500m、500m | B. | 500m、0m | C. | 500m、314m | D. | 614m、500m |
| A. | 只有体积很小的带电体,才能看作点电荷 | |
| B. | 体积很大的带电体一定不能看作点电荷 | |
| C. | 库仑定律适用于任何电荷间的相互作用 | |
| D. | 当两个带电体的大小及形状对它们之间相互作用力的影响可忽略时,两个带电体才可看成点电荷 |
| A. | 压力传感器 | B. | 温度传感器 | C. | 声音传感器 | D. | 红外线传感器 |
| A. | 胡克用逻辑推理的方法得出了胡克定律 | |
| B. | 亚里士多德认为力是改变物体运动状态的原因 | |
| C. | 牛顿做了著名的斜面实验,得出轻重物体自由下落一样快的结论 | |
| D. | 伽利略开创了科学实验之先河,他把科学的推理方法引入了科学研究 |
| A. | 运动员在前7s的平均速度大小是8.14m/s | |
| B. | 运动员在8s末的瞬时速度大小为9.2m/s | |
| C. | 运动员在百米全过程的平均速度大小是8.47m/s | |
| D. | 无法知道运动员在8s末的瞬时速度大小 |
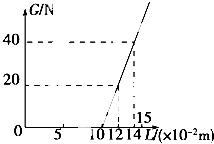 在“探究弹力与弹簧伸长的关系”的试验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,和用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示,根据图象回答以下问题:
在“探究弹力与弹簧伸长的关系”的试验中,某实验小组将不同数量的钩码分别挂在竖直弹簧下端,进行测量,根据实验所测数据,和用描点法作出了所挂钩码的重力G与弹簧总长L的关系图象,如图所示,根据图象回答以下问题: