题目内容
6. 如图所示,边长为L的正方形单匝线圈abcd,其电阻为r,外电路的电阻为R,ab的中点和cd的中点的连线O′O恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始以角速度ω绕轴O′O匀速转动,则以下判断正确的是( )
如图所示,边长为L的正方形单匝线圈abcd,其电阻为r,外电路的电阻为R,ab的中点和cd的中点的连线O′O恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始以角速度ω绕轴O′O匀速转动,则以下判断正确的是( )| A. | 图示位置线圈中的感应电动势最大为Em=BL2ω | |
| B. | 闭合电路中感应电动势的瞬时值表达式为e=$\frac{1}{2}$BL2ωsinωt | |
| C. | 线圈从图示位置转过180°的过程中,流过电阻R的电荷量为q=$\frac{B{L}^{2}}{R+r}$ | |
| D. | 线圈转动一周的过程中,电阻R上产生的热量为Q=$\frac{π{B}^{2}ω{L}^{4}R}{4(R+r)^{2}}$ |
分析 当线圈与磁场平行时感应电动势最大,由公式Em=BSω求解感应电动势的最大值.图中是中性面,线框在匀强磁场中匀速转动,产生正弦式交变电流,根据e=Emsinωt可列出感应电动势的瞬时表达式,根据感应电荷量q=$\frac{△Φ}{R+r}$,求通过电阻R的电荷量.最大值是有效值的$\sqrt{2}$倍,求得电动势有效值,根据焦耳定律求电量Q.
解答 解:A、图示位置线圈中没有任何一边切割磁感线,感应电动势为零,故A错误.
B、当线圈与磁场平行时感应电动势最大,最大值为Em=BSω=B$\frac{1}{2}{L}^{2}$ω,瞬时值表达式为e=Emsinωt=$\frac{1}{2}$BL2ωsinωt.故B正确.
C、线圈从图示位置转过180°的过程中,穿过线圈磁通量的变化量大小为△Φ=2BS=2B$•\frac{1}{2}{L}^{2}$=BL2,流过电阻R的电荷量为q=$\frac{△Φ}{R+r}$=$\frac{B{L}^{2}}{R+r}$,故C正确.
D、感应电动势的有效值为E=$\frac{\sqrt{2}}{2}{E}_{m}$,感应电流有效值为I=$\frac{E}{R+r}$,R产生的热量为Q=I2RT,T=$\frac{2π}{ω}$,联立得Q=$\frac{π{B}^{2}ω{L}^{4}R}{4(R+r)^{2}}$.故D正确.
故选:BCD.
点评 本题要掌握正弦式交变电流瞬时值表达式,注意计时起点,掌握感应电荷量的经验公式q=$\frac{△Φ}{R+r}$,知道用有效值求热量.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
14.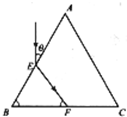 如图所示等边三棱镜截面ABC,有一束单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角θ=30°,E、F分别为边AB、BC的中点,则( )
如图所示等边三棱镜截面ABC,有一束单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角θ=30°,E、F分别为边AB、BC的中点,则( )
 如图所示等边三棱镜截面ABC,有一束单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角θ=30°,E、F分别为边AB、BC的中点,则( )
如图所示等边三棱镜截面ABC,有一束单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角θ=30°,E、F分别为边AB、BC的中点,则( )| A. | 该棱镜的折射率为$\sqrt{3}$ | |
| B. | 光在F点发生全反射 | |
| C. | 光从空气进入棱镜,波长变小 | |
| D. | 从F点出射的光束与入射到E点的光束平行 |
1.入射光照射到某金属表面上发生光电效应,若入射光强度减弱,而频率不变,则( )
| A. | 有可能不发生光电效应 | |
| B. | 逸出的光电子的最大初动能将减小 | |
| C. | 单位时间内从金属表面逸出的光电子数目将减小 | |
| D. | 从光照至金属表面上到发射出光电子之间的时间间隔将明显增加 |
15.某同学利用如图1装置研究物体以相同的初速度与不同质量的物体发生完全非弹性碰撞时的规律.器材:轻弹簧、刻度尺、材料相同的两物块m和M、砝码若干.实验前,将一水平滑槽固定在地面上,已知滑槽足够长,与物块间摩擦系数为μ(μ值较小).物块M的上表面有四个卡孔,每个卡孔可以放入一个砝码,从而方便在实验中改变被碰物体的质量.在物块M的左端粘上双面胶以保证m和M相碰后粘在一起运动,已知重力加速度为g.
实验步骤如下:

Ⅰ把轻弹簧一端固定在水平滑槽的左端,记录下弹簧自由端的位置O
Ⅱ放置物块M在某 C点处,记录下此C位置.用物块m压缩弹簧至某位置B处,记录下位置B,放手使物块m弹出,m和物块M碰撞后一起向右运动至停下,记录m和M碰后一起滑行的距离x
Ⅲ逐次在M上添加不同个数的砝码,重复几次Ⅱ,测出几个对应的x
已知m=20g,每个砝码的质量m0=5g,测量数据如表:
回答下列问题:
①每次实验都将M放在相同的C点,都让m压缩到相同的位置B再放手可以保正每次碰前m的速度相同(填“相同”或“不同”)
②若M在初始时按照图中的摆放方法,则测量x时,应测量C点到停下后M的右端(填“左端”或“右端”)间的距离
③利用碰撞后到停下的过程,可表示出碰后的速度为$\sqrt{2μgx}$(用g,x,μ表示)
④从表格中可以发现随着砝码个数增加,距离x变短,为找到定量规律,我们可以选用添加的砝码质量m1为纵坐标,$\frac{1}{\sqrt{x}}$(选填x、$\frac{1}{x}$、$\sqrt{x}$、$\frac{1}{\sqrt{x}}$)为横坐标,可做出如图2的直线函数图线.若延长得该直线的纵截距为-40g,则M的质量应为20g.
⑤利用③、④中的结论及表格中的任意一组数据,根据动量守恒定律,可以计算出m在碰前瞬间的速度.
实验步骤如下:

Ⅰ把轻弹簧一端固定在水平滑槽的左端,记录下弹簧自由端的位置O
Ⅱ放置物块M在某 C点处,记录下此C位置.用物块m压缩弹簧至某位置B处,记录下位置B,放手使物块m弹出,m和物块M碰撞后一起向右运动至停下,记录m和M碰后一起滑行的距离x
Ⅲ逐次在M上添加不同个数的砝码,重复几次Ⅱ,测出几个对应的x
已知m=20g,每个砝码的质量m0=5g,测量数据如表:
| 砝码数/个 | 0 | 1 | 2 | 3 | 4 |
| x(cm) | 100.00 | 44.40 | 25.00 | 16.01 | 11.10 |
| $\frac{1}{x}$(cm-1) | 0.010 | 0.023 | 0.040 | 0.063 | 0.090 |
| $\sqrt{x}$(cm0.5) | 10.00 | 6.70 | 5.00 | 4.00 | 3.30 |
| $\frac{1}{\sqrt{x}}$(cm-0.5) | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
①每次实验都将M放在相同的C点,都让m压缩到相同的位置B再放手可以保正每次碰前m的速度相同(填“相同”或“不同”)
②若M在初始时按照图中的摆放方法,则测量x时,应测量C点到停下后M的右端(填“左端”或“右端”)间的距离
③利用碰撞后到停下的过程,可表示出碰后的速度为$\sqrt{2μgx}$(用g,x,μ表示)
④从表格中可以发现随着砝码个数增加,距离x变短,为找到定量规律,我们可以选用添加的砝码质量m1为纵坐标,$\frac{1}{\sqrt{x}}$(选填x、$\frac{1}{x}$、$\sqrt{x}$、$\frac{1}{\sqrt{x}}$)为横坐标,可做出如图2的直线函数图线.若延长得该直线的纵截距为-40g,则M的质量应为20g.
⑤利用③、④中的结论及表格中的任意一组数据,根据动量守恒定律,可以计算出m在碰前瞬间的速度.
16. 小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
 小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )| A. | 能判定位置“1”是小球释放的初始位置 | |
| B. | 能求出小球下落的加速度大小为a=$\frac{d}{4{T}^{2}}$ | |
| C. | 能求出小球在位置“3”的速度大小为V=$\frac{7d}{T}$ | |
| D. | 如果再知道当地的重力加速度,就可以验证小球下落过程中机械能是否守恒 |


 质量为m=2kg的两平板车M和N靠在一起且静止在光滑水平面上,两平板车的上表面在同一高度且表面粗糙,在M车的左端静止着质量为mA=2kg的物体A(可视为质点),如图所示,一颗质量为mB=20g的子弹以800m/s的水平速度射穿A后,速度变为100m/s,当物体A从M车滑到N车上时,M车与N车立即分开,最后物体A与N车具有相同的速度vAN=3m/s,求物体A在M车的左端和右端的速度分别是多大.
质量为m=2kg的两平板车M和N靠在一起且静止在光滑水平面上,两平板车的上表面在同一高度且表面粗糙,在M车的左端静止着质量为mA=2kg的物体A(可视为质点),如图所示,一颗质量为mB=20g的子弹以800m/s的水平速度射穿A后,速度变为100m/s,当物体A从M车滑到N车上时,M车与N车立即分开,最后物体A与N车具有相同的速度vAN=3m/s,求物体A在M车的左端和右端的速度分别是多大. 如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经t=3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,不计空气阻力.(已知sin37°=0.6)求:
如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经t=3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,不计空气阻力.(已知sin37°=0.6)求: