题目内容
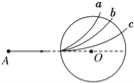
【题目】如图所示,在竖直平面内有一质量m=0.6kg、电荷量g=+3×10-3C的带电的小球,用一根长L=0.2m且不可伸长的绝缘轻细线系在一方向水平向右、分布的区域足够大的匀强电场中的O点。已知A、O、C三点等高,且OA=OC=L,若将带电小球从A点无初速度释放,小球到达最低点B时速度恰好为零,取g=10m/s2。

(1)求匀强电场的电场强度E的大小;
(2)求小球从A点由静止释放运动到B点的过程中速度最大时细线的拉力大小;.
(3)若将带电小球从C点无初速度释放,求小球到达A点时的速度。
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】(1)小球到达最低点B时速度为0,根据动能定理有:![]()
解得:![]()
(2)小球到达最低点B时速度为0,根据对称性可知,达到最大速度的位置为AB弧的中点,即当沿轨迹上任一点切线方向的合力为零时,物体的速度有极值
根据动能定理有:![]()
根据牛顿第二定律有:![]()
联立解得:![]() (或
(或![]() )
)
(3)小球从C点运动到B点做匀加速直线运动,则有:
![]() ,
,![]() ,
,![]()
到达B点后细线绷直有机械能的损失,![]()
小球由B→A过程中,根据动能定理有:![]()
解得:![]()

练习册系列答案
相关题目