题目内容
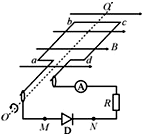 如图所示,一个小型旋转式交流发电机,其矩形线圈的线框面积为S,共有n匝,总电阻为r,外电路上接有一个阻值为R的定值电阻、理想交流电流表A和二极管D.线圈以角速度ω在磁感应强度为B的匀强磁场中绕与磁场方向垂直的对称轴OO′匀速运动,下列说法正确的是( )
如图所示,一个小型旋转式交流发电机,其矩形线圈的线框面积为S,共有n匝,总电阻为r,外电路上接有一个阻值为R的定值电阻、理想交流电流表A和二极管D.线圈以角速度ω在磁感应强度为B的匀强磁场中绕与磁场方向垂直的对称轴OO′匀速运动,下列说法正确的是( )A、一个周期内通过R的电荷量q=
| ||
B、R两端电压的有效值U=
| ||
| C、交流电流表的示数一直在变化 | ||
| D、若用一根导线连接M、N两点,电阻R上的功率不变 |
分析:根据法拉第电磁感应定律、欧姆定律和电流的定义式求解电量;从图示位置磁通量为Φ1=0,转过90°磁通量为Φ2=BS,△Φ=Φ2-Φ1;交流电流表测量有效值,由电动势的最大值、欧姆定律和有效值与最大值之间的关系求解电压的有效值.
解答:解:A、由于二极管的单向导电性,一个周期内只有半个周期有电流流过电阻R,根据法拉第电磁感应定律,有:
=N
=n
=
故通过R的电荷为:
q=
t=
?
=
,故A正确;
B、电动势的最大值为:Em=nBSω,故有效值为:E=
=
;
由于二极管的单向导电性,一个周期内只有半个周期有电流流过电阻R,根据热效应,有:
?T=(
)2?
其中:E=
解得:U=
,故B正确;
C、交流电流表测量有效值,示数不变,故C错误;
D、由于二极管的单向导电性,一个周期内只有半个周期有电流流过电阻R;
若用一根导线连接M、N两点,一个周期内一直有电流流过电阻R,故电功率会加倍,故D错误;
故选:AB.
. |
| E |
| △Φ |
| △t |
| 2BS | ||
|
| 4nBS |
| T |
故通过R的电荷为:
q=
. |
| I |
| ||
| R+r |
| T |
| 2 |
| 2nBS |
| R+r |
B、电动势的最大值为:Em=nBSω,故有效值为:E=
| Em | ||
|
| ||
| 2 |
由于二极管的单向导电性,一个周期内只有半个周期有电流流过电阻R,根据热效应,有:
| U2 |
| R |
| E |
| R+r |
| T |
| 2 |
其中:E=
| ||
| 2 |
解得:U=
| nBSωR |
| 2(R+r) |
C、交流电流表测量有效值,示数不变,故C错误;
D、由于二极管的单向导电性,一个周期内只有半个周期有电流流过电阻R;
若用一根导线连接M、N两点,一个周期内一直有电流流过电阻R,故电功率会加倍,故D错误;
故选:AB.
点评:对于交变电流,求解热量、电功和电功率用有效值,而求解电量要用平均值,注意二极管D具有单向导电性,难度不大.

练习册系列答案
相关题目