题目内容
正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段。
(1)PET在心脏疾病诊疗中,需要使用放射正电子的同位素氮13示踪剂。氮13是由小型回旋加速器输出的高速质子轰击氧16获得的,反应中同还产生另一个粒子,试写出该核反应方程。
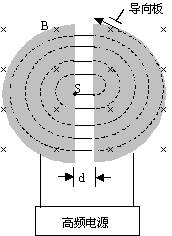
(2)PET所用回旋加速器示意如图,其中置于高真空中的金属D形盒的半径为R,两盒间距为d,在左侧D形盒圆心处放有粒子源S,匀强磁场的磁感应强度为B,方向如图所示。质子质量为m,电荷量为q。设质子从粒子源S进入加速电场时的初速度不计,质子在加速器中运动的总时间为t(其中已略去了质子在加速电场中的运动时间),质子在电场中的加速次数与加旋半周的次数相同,加速电子时的电压大小可视为不变。求此时加速器所需的高频电源频率f和加速电压U。
(3)试推证当R>>d时,质子在电场中加速的总时间相对于在D形盒中回旋的总时间可忽略不计(质子在电场中运动时,不考虑磁场的影响)。
答案:
解析:
解析:
解: (1)核反应方程为+→+ (2)设质子加速后最大速度为v,由牛顿第二定律有 qvB=m 质子的回旋周期 T== 高频电源的频率 f== 质子加速后的最大动能 Ek=mv2 设质子在电场中加速的次数为n,则 Ek=nqU 又 t=n 可解得 U= (3)在电场中加速的总时间为 t1== 在D形盒中回旋的总时间为 t2=n 故 =<<1 即当R>>d时,t1可忽略不计。
|

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 (1)下列说法正确的有
(1)下列说法正确的有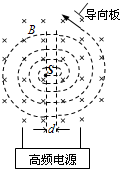 正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.
正电子发射计算机断层(PET)是分子水平上的人体功能显像的国际领先技术,它为临床诊断和治疗提供全新的手段.