题目内容
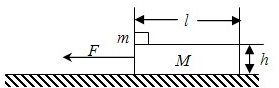
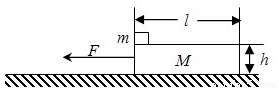
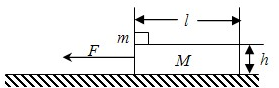 如图所示,长为l=2.0m、高为h=0.2m、质量为M=2kg的木板静止在水平地面上,它与地面间的动摩擦因数为μ1=0.2,在木板的左端放一质量为m=1kg的小铁块(可视为质点),铁块与木板间的动摩擦因数为μ2=0.1,现以F=11N的水平拉力向左拉动木板,g=10m/s2,求:
如图所示,长为l=2.0m、高为h=0.2m、质量为M=2kg的木板静止在水平地面上,它与地面间的动摩擦因数为μ1=0.2,在木板的左端放一质量为m=1kg的小铁块(可视为质点),铁块与木板间的动摩擦因数为μ2=0.1,现以F=11N的水平拉力向左拉动木板,g=10m/s2,求:(1)木板运动时的加速度;
(2)经过多长时间小铁块将从木板右端脱落.
分析:(1)用力F拉动木板时,小铁块相对木板滑动,对木板进行受力分析,根据牛顿第二定律即可求解;
(2)先求出小铁块的加速度,小铁块和木板都做匀变速运动,根据两者位移的关系即可列式求解.
(2)先求出小铁块的加速度,小铁块和木板都做匀变速运动,根据两者位移的关系即可列式求解.
解答:解:(1)对木板进行受力分析,根据牛顿第二定律得:
F-μ1(M+m)g-μ2mg=MaM
带入数据得:aM=2m/s2
(2)对小铁块由牛顿第二定律得:
μ2mg=mam
解得:a1=1m/s2
设经过t时间铁块脱落,由匀变速运动公式得:
l=
aMt2-
amt2
解得:t=2s
答:(1)木板运动时的加速度为2m/s2;
(2)经过2s小铁块将从木板右端脱落.
F-μ1(M+m)g-μ2mg=MaM
带入数据得:aM=2m/s2
(2)对小铁块由牛顿第二定律得:
μ2mg=mam
解得:a1=1m/s2
设经过t时间铁块脱落,由匀变速运动公式得:
l=
| 1 |
| 2 |
| 1 |
| 2 |
解得:t=2s
答:(1)木板运动时的加速度为2m/s2;
(2)经过2s小铁块将从木板右端脱落.
点评:本题主要考查了牛顿第二定律的直接应用,抓住两者位移直接的关系列式可求脱离时间,难度不大.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
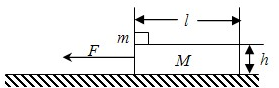 如图所示,长为l=2.0m、高为h=0.2m、质量为M=2kg的木板静止在水平地面上,它与地面间的动摩擦因数为μ1=0.2,在木板的左端放一质量为m=1kg的小铁块(可视为质点),铁块与木板间的动摩擦因数为μ2=0.1,现以F=11N的水平拉力向左拉动木板,g=10m/s2,求:
如图所示,长为l=2.0m、高为h=0.2m、质量为M=2kg的木板静止在水平地面上,它与地面间的动摩擦因数为μ1=0.2,在木板的左端放一质量为m=1kg的小铁块(可视为质点),铁块与木板间的动摩擦因数为μ2=0.1,现以F=11N的水平拉力向左拉动木板,g=10m/s2,求: