题目内容
【题目】如图，光滑绝缘半球槽的半径为R，处在水平向右的匀强电场中，一质量为m的带电小球从槽的右端A处无初速沿轨道滑下，滑到最低点B时，球对轨道的压力为2mg。求
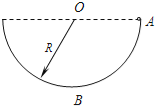
（1）小球受到的电场力的大小和方向。
（2）带电小球在滑动过程中的最大速度。
【答案】(1) 
,方向水平向右 （2）
【解析】试题分析：（1）设小球运动到最底位置B时速度为v，此时
①
解得：
若不受电场力，则：
解得：
因为
所以此过程中电场力做负功，电场力方向水平向右
设电场力大小为F，由题意，小球从A处沿槽滑到最底位置B的过程中，根据动能定理得：
②
由①、②两式得：
③，方向水平向右
（2）小球在滑动过程中最大速度的条件：是小球沿轨道运动过程某位置时切向合力为零，设此时小球和圆心间的连线与竖直方向的夹角为θ，如图
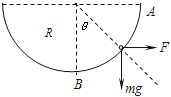
④
由④得：
小球由A处到最大速度位置得过程中
得： 
练习册系列答案
相关题目
【题目】为验证动能定理，某同学设计了如下实验．将一长直木板一端垫起，另一端侧面装一速度传感器，让小滑块由静止从木板h高处（从传感器所在平面算起）自由滑下至速度传感器时，读出滑块经此处时的速度v，如图所示．多次改变滑块的下滑高度h（斜面的倾角不变），对应的速度值记录在表中：
下滑高度h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
速度v/ms﹣1 | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
要最简单直观地说明此过程动能定理是否成立，该同学建立了以h为纵轴的坐标系，你认为坐标系的横轴应该是 ， 本实验是否需要平衡摩擦力（填“是”或“否”）．
