题目内容
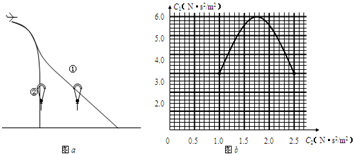
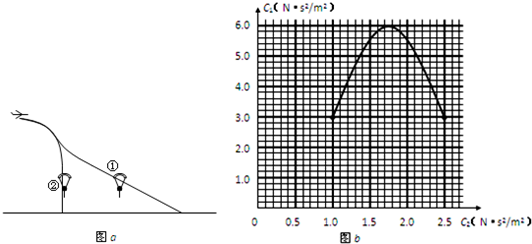
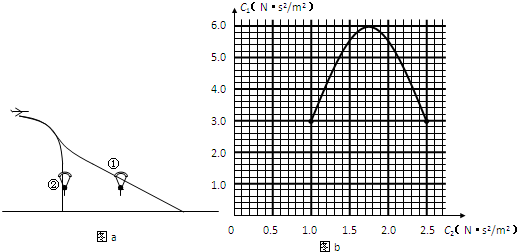
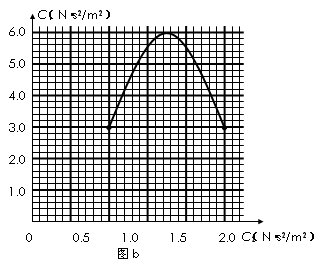
 翼型降落伞有很好的飞行性能.它被看作飞机的机翼,跳伞运动员可方便地控制转弯等动物.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2.其中C1.C2相互影响,可由运动员调节,满足如图b所示的关系.试求:
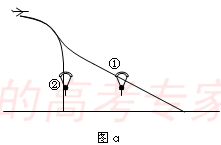
翼型降落伞有很好的飞行性能.它被看作飞机的机翼,跳伞运动员可方便地控制转弯等动物.其原理是通过对降落伞的调节,使空气升力和空气摩擦力都受到影响.已知:空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气摩擦力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2.其中C1.C2相互影响,可由运动员调节,满足如图b所示的关系.试求:(1)图a中画出了运动员携带翼型伞跳伞后的两条大致运动轨迹.试对两位置的运动员画出受力示意图并判断,①.②两轨迹中哪条是不可能的,并简要说明理由;
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,试从力平衡的角度证明:tanα=C2/C1;
(3)某运动员和装备的总质量为70kg,匀速飞行的速度v与地平线的夹角α约20°取tan20°=4/11.,匀速飞行的速度v多大?g取10m/s2,结果保留3位有效数字.
(4)若运动员出机舱时飞机距地面的高度为800m.飞机飞行速度为540km/h,降落过程中该运动员和装备损失的机械能△E多大?
分析:(1)物体做直线运动的条件是所受的合力方向与速度方向在一条直线上,根据运动员和翼型伞的受力情况进行判断;
(2)由①位置的受力分析,匀速运动时对重力进行分解,根据平衡条件求解;
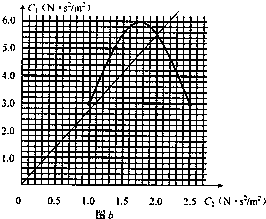
(3)在图b中过原点作直线C2=
C1,正确得到直线与曲线的交点后求解.
(4)根据初末状态的机械能之差求解降落过程中该运动员和装备损失的机械能△E.
(2)由①位置的受力分析,匀速运动时对重力进行分解,根据平衡条件求解;
(3)在图b中过原点作直线C2=
| 4 |
| 11 |
(4)根据初末状态的机械能之差求解降落过程中该运动员和装备损失的机械能△E.
解答:解:(1)因为最终匀速行驶时,有tanα=
.α为飞行的速度v与地平线的夹角.根据图线C1、C2的关系,知最终匀速行驶时,α不可能等于90°.故②轨迹不可能存在.
①位置,三力可能平衡(或三力的合力可能与速度在一直线),运动员做直线运动.
②位置,合力方向与速度方向不可能在一直线,所以不会沿竖直方向做直线运动.
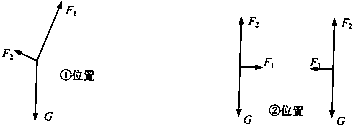
(2)由①位置的受力分析可知,匀速运动时
F=mgcosα=C1v2…(1)
F=mgsinα=C2v2…(2)
两式消去mg和v得tanα=
(3)在图b中过原点作直线正确得到直线与曲线的交点
C2=2,C1=5.5(5.5~5.6均正确)
根据F2=mgsinα=C2v2或F1=mgcosα=C1v2(上两式任取其一)
得:v=10.9m/s(在10.7~11.0之间均可)
(4)降落过程中该运动员和装备损失的机械能:△E=mgH+
m
-
mv2=(70×10×800+
×70×1502-
×70×10.92)J
=1.34×106J
答:
(1)画出受力示意图见上,②轨迹不可能存在,
①位置,三力可能平衡(或三力的合力可能与速度在一直线),运动员做直线运动.
②位置,合力方向与速度方向不可能在一直线,所以不会沿竖直方向做直线运动.
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,从力平衡的角度证明见上.
(3)匀速飞行的速度v为10.9m/s.
(4)降落过程中该运动员和装备损失的机械能△E为1.34×106J.
| C2 |
| C1 |
①位置,三力可能平衡(或三力的合力可能与速度在一直线),运动员做直线运动.
②位置,合力方向与速度方向不可能在一直线,所以不会沿竖直方向做直线运动.
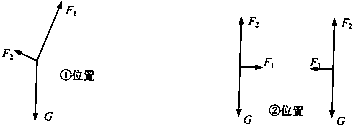
(2)由①位置的受力分析可知,匀速运动时
F=mgcosα=C1v2…(1)
F=mgsinα=C2v2…(2)
两式消去mg和v得tanα=
| C2 |
| C1 |
(3)在图b中过原点作直线正确得到直线与曲线的交点
C2=2,C1=5.5(5.5~5.6均正确)
根据F2=mgsinα=C2v2或F1=mgcosα=C1v2(上两式任取其一)
得:v=10.9m/s(在10.7~11.0之间均可)
(4)降落过程中该运动员和装备损失的机械能:△E=mgH+
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1.34×106J

答:
(1)画出受力示意图见上,②轨迹不可能存在,
①位置,三力可能平衡(或三力的合力可能与速度在一直线),运动员做直线运动.
②位置,合力方向与速度方向不可能在一直线,所以不会沿竖直方向做直线运动.
(2)若降落伞最终匀速飞行的速度v与地平线的夹角为α,从力平衡的角度证明见上.
(3)匀速飞行的速度v为10.9m/s.
(4)降落过程中该运动员和装备损失的机械能△E为1.34×106J.
点评:本题有一定的难度,能正确的理解题目所提示的信息,并有一定的数据解读能力是解决该题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目