题目内容
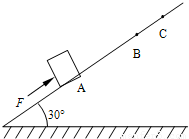
如图，小木块在倾角为300的斜面上受到与斜面平行向上的恒定外力F作用，从A点由静止开始做匀加速运动，前进了0.45m抵达B点时，立即撤去外力，此后小木块又前进0.15m到达C点，速度为零．已知木块与斜面动摩擦因数μ=
/6，木块质量m=1kg．求：
（1）木块在BC段加速度的大小；
（2）木块向上经过B点时速度大小；
（3）木块在AB段所受的外力F大小．（ g=10m/s2）
解：
（1）木块在BC段受到重力、斜面的支持力和滑动摩擦力，根据牛顿第二定律得：
mgsin30°+μmgcos30°=maBC
解得aBC=gsin30°+μgcos30°=7.5m/s2
（2）由vc2-vB2=2aBCxBC
解得：vB=1.5m/s
（3）A→B过程：vB2-vA2=2aABxAB
解得aAB=2.5 m/s2
木块在AB段受到重力、外力F，斜面的支持力和滑动摩擦力．
F-mgsin30°-μmgcos30°=maAB
代入数据解得：F=10N
答：（1）木块在BC段加速度的大小为7.5m/s2；
（2）木块向上经过B点时速度大小为1.5m/s；
（3）木块在AB段所受的外力F大小为10N．
分析：（1）木块在BC段受到重力、斜面的支持力和滑动摩擦力，根据牛顿第二定律求解加速度．
（2）由速度与位移关系公式求出木块向上经过B点时速度大小．
（3）木块在AB段受到重力、外力F，斜面的支持力和滑动摩擦力．先由初速度、位移和末速度求出加速度，再由牛顿第二定律外力F．
点评：本题是牛顿第二定律与运动学公式的综合应用，也可以根据动能定理研究第（2）问和第（3）问．
（1）木块在BC段受到重力、斜面的支持力和滑动摩擦力，根据牛顿第二定律得：
mgsin30°+μmgcos30°=maBC
解得aBC=gsin30°+μgcos30°=7.5m/s2
（2）由vc2-vB2=2aBCxBC
解得：vB=1.5m/s
（3）A→B过程：vB2-vA2=2aABxAB
解得aAB=2.5 m/s2
木块在AB段受到重力、外力F，斜面的支持力和滑动摩擦力．
F-mgsin30°-μmgcos30°=maAB
代入数据解得：F=10N
答：（1）木块在BC段加速度的大小为7.5m/s2；
（2）木块向上经过B点时速度大小为1.5m/s；
（3）木块在AB段所受的外力F大小为10N．
分析：（1）木块在BC段受到重力、斜面的支持力和滑动摩擦力，根据牛顿第二定律求解加速度．
（2）由速度与位移关系公式求出木块向上经过B点时速度大小．
（3）木块在AB段受到重力、外力F，斜面的支持力和滑动摩擦力．先由初速度、位移和末速度求出加速度，再由牛顿第二定律外力F．
点评：本题是牛顿第二定律与运动学公式的综合应用，也可以根据动能定理研究第（2）问和第（3）问．
练习册系列答案
名校课堂系列答案
相关题目
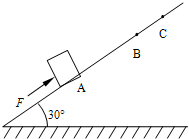
如图，小木块在倾角为300的斜面上受到与斜面平行向上的恒定外力F作用，从A点由静止开始做匀加速运动，前进了0.45m抵达B点时，立即撤去外力，此后小木块又前进0.15m到达C点，速度为零．已知木块与斜面动摩擦因数μ=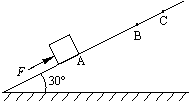
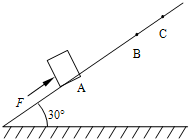
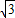
/6，木块质量m=1kg。求：
/6，木块质量m=1kg．求：