题目内容
【题目】某同学用下面的方法做“探究功与速度变化的关系”的实验,将木板固定在水平的 桌面上,在木板虚线PP'上钉两个钉子,木块上钉一个钉子,橡皮筋两端分别固定 在木板的钉子上。现将木块拉至虚线00’处,释放木块,设其前端到达PP'时速度 为v,木块离开橡皮筋后滑行的距离为s
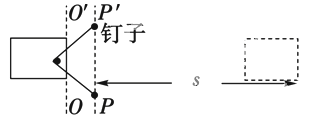
(1)如果用一根橡皮筋将木块拉到OO'处,释放木块,橡皮筋对木块做的功为W, 那么,当把三根相同的橡皮筋并起来将木块拉到00'处,释放木块,橡皮筋对 物体所做的功为 (图中两虚线间距离很小,摩擦不计);
(2)用1, 2, 3, 4, 5根橡皮筋分别对木块做功,测得木块离开橡皮筋后滑行的距 离为S1,S2, S3, S4, S5。以橡皮筋对木块做的功W为纵坐标,以滑行的距离S 为横坐标,作出W-s图象是过原点的直线,那么W与v的关系是_____。
【答案】![]()
![]() 与
与![]() 成正比
成正比
【解析】(1)橡皮筋对物体所做的功为与橡皮筋的条数成正比,则当把三根相同的橡皮筋并起来将木块拉到![]() 处,释放木块,橡皮筋对物体所做的功为
处,释放木块,橡皮筋对物体所做的功为![]() ;
;
(2)测得木块离开橡皮筋后做匀减速直线运动,根据牛顿第二定律![]()
滑行的距离![]() ,即
,即![]() ,由题作出
,由题作出![]() 图象是过原点的直线,即
图象是过原点的直线,即![]()
故W与v的关系是![]() 。
。

练习册系列答案
相关题目