题目内容
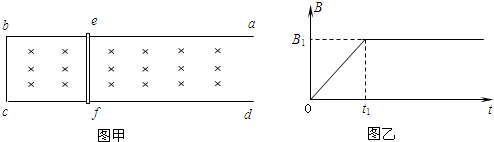
如图甲所示，固定于水平桌面上足够长的光滑金属导轨abcd，金属棒ef搁在导轨上，bcfe构成一个边长为L的正方形，金属棒的电阻为r，其余的电阻不计．在t=0的时刻，导轨间加一竖直向下的匀强磁场，磁感应强度随时间的变化如图乙所示．为使金属棒ef在0-t1时间内保持静止，在金属棒ef上施加一水平拉力F，从t1时刻起保持此时的水平拉力F不变，金属棒ef在导轨上运动了位移s时刚好达到最大速度，求：
（1）在t=t1时刻水平拉力F的大小和方向；
（2）金属棒ef在导轨上运动的最大速度；
（3）从t=0开始到金属棒ef达到最大速度的过程中，金属棒ef中产生的热量．
（1）在t=t1时刻水平拉力F的大小和方向；
（2）金属棒ef在导轨上运动的最大速度；
（3）从t=0开始到金属棒ef达到最大速度的过程中，金属棒ef中产生的热量．
分析：（1）由法拉第电磁感应定律求出感应电动势，由F=BIL求出安培力，由楞次定律判断出感应电流的方向，由左手定则判断出安培力的方向，由平衡条件求出拉力大小与方向；
（2）当拉力与安培力相等时，导体棒做匀速运动，速度达到最大，求出拉力，根据安培力公式求出导体棒的最大速度；
（3）由焦耳定律求出导体棒静止时产生的焦耳热，由能量守恒定律求出导体棒运动时产生的焦耳热，然后求出整个过程产生的焦耳热．
（2）当拉力与安培力相等时，导体棒做匀速运动，速度达到最大，求出拉力，根据安培力公式求出导体棒的最大速度；
（3）由焦耳定律求出导体棒静止时产生的焦耳热，由能量守恒定律求出导体棒运动时产生的焦耳热，然后求出整个过程产生的焦耳热．
解答：解：（1）在t=t1时刻，拉力等于安培力．
根据法拉第电磁感应定律有：E=
S=
．
则电流为：I=
=
．
则拉力为：F=BIL=B1?
L=
．
根据楞次定律知，感应电流的方向为逆时针方向，根据左手定则知，安培力的方向水平向左．则拉力的方向水平向右．
（2）当拉力等于安培力时，速度最大．
有F=B1IL=
，又F=
解得：v=
．
（3）导体棒静止时，产生的焦耳热为：Q1=I2rt1
．
金属棒从开始运动到最大速度阶段，由能量守恒定律，得：
Q2=Fs-
mv2=
-
则全过程产生的焦耳热为：
Q=Q1+Q2=
-
．
答：（1）在t=t1时刻水平拉力F的大小为
，方向水平向右．
（2）金属棒ef在导轨上运动的最大速度为
．
（3）从t=0开始到金属棒ef达到最大速度的过程中，金属棒ef中产生的热量为
-
．
根据法拉第电磁感应定律有：E=
| △B |
| △t |
| B1L2 |
| t1 |
则电流为：I=
| E |
| r |
| B1L2 |
| rt1 |
则拉力为：F=BIL=B1?
| B1L2 |
| rt1 |
| B12L3 |
| rt1 |
根据楞次定律知，感应电流的方向为逆时针方向，根据左手定则知，安培力的方向水平向左．则拉力的方向水平向右．
（2）当拉力等于安培力时，速度最大．
有F=B1IL=
| B12L2v |
| r |
| B12L3 |
| rt1 |
解得：v=
| L |
| t1 |
（3）导体棒静止时，产生的焦耳热为：Q1=I2rt1
| B12L4 |
| rt1 |
金属棒从开始运动到最大速度阶段，由能量守恒定律，得：
Q2=Fs-
| 1 |
| 2 |
| B12L3s |
| rt1 |
| mL2 |
| 2t12 |
则全过程产生的焦耳热为：
Q=Q1+Q2=
| B12L3(L+s) |
| rt1 |
| mL2 |
| 2t12 |
答：（1）在t=t1时刻水平拉力F的大小为
| B12L3 |
| rt1 |
（2）金属棒ef在导轨上运动的最大速度为
| L |
| t1 |
（3）从t=0开始到金属棒ef达到最大速度的过程中，金属棒ef中产生的热量为
| B12L3(L+s) |
| rt1 |
| mL2 |
| 2t12 |
点评：本题综合考查了法拉第电磁感应定律、切割产生的感应电动势公式等，关键理清导体棒的运动的运动规律，知道拉力等于安培力时，速度最大．
练习册系列答案
相关题目
时刻起保持此时的水平拉力F不变，金属棒ef在导轨上运动了s后刚好达到最大速度，求：
时刻该水平拉力F的大小和方向；
时刻起保持此时的水平拉力F不变，金属棒ef在导轨上运动了s后刚好达到最大速度，求：
时刻该水平拉力F的大小和方向；