��Ŀ����
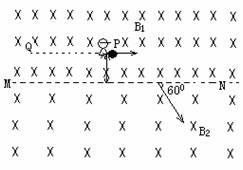
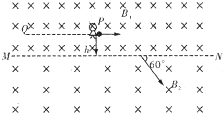 ��ͼ�Ǽ����ģ�����һ������ռ���龳���ڴ�����ռ��������һ��Զ�������ռ��������MNΪ�磬�ϲ�����ǿ�ų��ĴŸ�Ӧǿ��ΪB1���²�����ǿ�ų��ĴŸ�Ӧǿ��ΪB2��B1=2B2=2B0��������ͬ���Ҵų������㹻���ھ������Ϊh��P����һ�Ա���ھ�ֹ״̬���Ա��ƽ���ڽ��ߵ��ٶ��׳�һ����Ϊm��������Ϊ-q��С�������ڽ��ߴ��ٶȷ�������߳�60��ǽ����²��ִų���Ȼ���Ա�������ƽ�е�ֱ�����ٵ���Ŀ��Q��ʱ���պ��ֽ�ס�����ֹ����
��ͼ�Ǽ����ģ�����һ������ռ���龳���ڴ�����ռ��������һ��Զ�������ռ��������MNΪ�磬�ϲ�����ǿ�ų��ĴŸ�Ӧǿ��ΪB1���²�����ǿ�ų��ĴŸ�Ӧǿ��ΪB2��B1=2B2=2B0��������ͬ���Ҵų������㹻���ھ������Ϊh��P����һ�Ա���ھ�ֹ״̬���Ա��ƽ���ڽ��ߵ��ٶ��׳�һ����Ϊm��������Ϊ-q��С�������ڽ��ߴ��ٶȷ�������߳�60��ǽ����²��ִų���Ȼ���Ա�������ƽ�е�ֱ�����ٵ���Ŀ��Q��ʱ���պ��ֽ�ס�����ֹ������1��С���ڴŸ�Ӧǿ��ΪB1��B2�Ĵų��еİ뾶�ֱ�Ϊ���٣������С���ڴų��е��ٶȴ�С��
��2��PQ������Ƕ��
��3��С���P�㵽Q���ʱ�䣮
��������1�������ڴų����˶��켣��ͼ��ʾ���ɼ���֪ʶ����켣�İ뾶����ţ�ٵڶ��������С���ڴų��е��ٶȴ�С��
��2�����ݹ켣�ĶԳ��ԣ��ɼ���֪ʶ���PQ��ľ��룮
��3�������켣����Ӧ��Բ�Ľǣ��õ�ʱ�������ڵĹ�ϵ���������С���P�㵽Q���ʱ�䣮
��2�����ݹ켣�ĶԳ��ԣ��ɼ���֪ʶ���PQ��ľ��룮
��3�������켣����Ӧ��Բ�Ľǣ��õ�ʱ�������ڵĹ�ϵ���������С���P�㵽Q���ʱ�䣮
����⣺��1�������ڴų����˶��켣��ͼ��ʾ���ɼ���֪ʶ��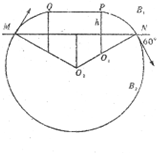
R1-h=R1cos60�㣬�� R1=2h
����qv��2B0��=m
��ã�v=
��ţ�ٵڶ����ɵã�
qvB=m
���ã�R=
����B1=2B2����ã�R2=2R1=4h
��2�����ݹ켣�ĶԳ��ԣ��õ�PQ��ľ���Ϊ��
l=2��R2sin60��-R1sin60�㣩=2
h
��3��С���P�㵽Q���ʱ��Ϊ��t=
+
=
?
+
?
=
��
��
��1��С���ڴŸ�Ӧǿ��B1��B2�Ĵų��еİ뾶�ֱ�Ϊ2h��4h��С���ڴų��е��ٶȴ�С��
��
��2��PQ�������2
h��
��3��С���P�㵽Q���ʱ����
��

R1-h=R1cos60�㣬�� R1=2h
����qv��2B0��=m
| v2 |
| R1 |
��ã�v=
| 4qB0h |
| m |
��ţ�ٵڶ����ɵã�
qvB=m
| v2 |
| R |
| mv |
| qB |
����B1=2B2����ã�R2=2R1=4h
��2�����ݹ켣�ĶԳ��ԣ��õ�PQ��ľ���Ϊ��
l=2��R2sin60��-R1sin60�㣩=2
| 3 |
��3��С���P�㵽Q���ʱ��Ϊ��t=
| T1 |
| 3 |
| 2T2 |
| 3 |
| 1 |
| 2 |
| 2��m |
| q(2B0) |
| 2 |
| 3 |
| 2��m |
| qB0 |
| 5��m |
| 3qB0 |
��
��1��С���ڴŸ�Ӧǿ��B1��B2�Ĵų��еİ뾶�ֱ�Ϊ2h��4h��С���ڴų��е��ٶȴ�С��
| 4qB0h |
| m |
��2��PQ�������2
| 3 |
��3��С���P�㵽Q���ʱ����
| 5��m |
| 3qB0 |
����������������ӱ���龰��ʵ���Ǵ��������ڴų����˶������ͣ������켣�����ݹ켣�ĶԳ��ԣ��ɼ���֪ʶ����켣�İ뾶�ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
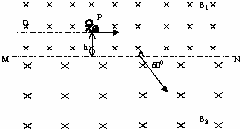 ��ͼ�Ǽ����ģ�����һ������ռ���龳���ڴ�����ռ��������һ��Զ�������ռ��������MNΪ�磬�ϲ�����ǿ�ų��ĴŸ�ǿ��ΪB1���²��ֵ���ǿ�ų��ĴŸ�ǿ��ΪB2��B1=2B2=2B0��������ͬ���Ҵų������㹻���ھ������Ϊh��P����һ�Ա���ھ�ֹ״̬���Ա��ƽ���ڽ��ߵ��ٶ��׳�һ����Ϊm��������-q��С�������ڽ��ߴ��ٶȷ�������߳�60��ǣ������²��ִų���Ȼ���Ա�������ƽ�е�ֱ�����ٵ���Ŀ��Q��ʱ���պ��ֽ�ס�����ֹ����
��ͼ�Ǽ����ģ�����һ������ռ���龳���ڴ�����ռ��������һ��Զ�������ռ��������MNΪ�磬�ϲ�����ǿ�ų��ĴŸ�ǿ��ΪB1���²��ֵ���ǿ�ų��ĴŸ�ǿ��ΪB2��B1=2B2=2B0��������ͬ���Ҵų������㹻���ھ������Ϊh��P����һ�Ա���ھ�ֹ״̬���Ա��ƽ���ڽ��ߵ��ٶ��׳�һ����Ϊm��������-q��С�������ڽ��ߴ��ٶȷ�������߳�60��ǣ������²��ִų���Ȼ���Ա�������ƽ�е�ֱ�����ٵ���Ŀ��Q��ʱ���պ��ֽ�ס�����ֹ����