题目内容
10. 在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求:
在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求:(1)M、N两点间的电势差UMN;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t.
分析 (1)粒子垂直于电场进入第一象限,粒子做类平抛运动,由速度的分解求出粒子到达x轴的速度大小,再用动能定理即可求得电场中M、N两点间的电势差.
(2)粒子以此速度进入第四象限,在洛伦兹力的作用下做匀速圆周运动,利用洛伦兹力提供向心力的公式,可由牛顿第二定律求出在磁场中运动的半径r.
(3)电场中,根据分位移公式求时间.磁场中,根据轨迹对应的圆心角求时间,即可得到总时间.
解答  解:(1)粒子垂直于电场进入第一象限,粒子做类平抛运动,将到达N点的速度分解得知
解:(1)粒子垂直于电场进入第一象限,粒子做类平抛运动,将到达N点的速度分解得知
vcosθ=v0
解得,粒子离开电场时的速度大小 v=2v0.
从M→N过程,由动能定理得:
qUMN=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02
代入解得,UMN=$\frac{3m{v}_{0}^{2}}{2q}$
(2)粒子进入第四象限后,在洛伦兹力的作用下做匀速圆周运动,则
qvB=m$\frac{{v}^{2}}{r}$
得粒子在磁场中做圆周运动的轨道半径为 r=$\frac{mv}{qB}$=$\frac{2m{v}_{0}}{qB}$
(3)画出轨迹如图,由几何知识得:ON=rsin60°
粒子从M点到N点的时间 t1=$\frac{ON}{{v}_{0}}$=$\frac{\sqrt{3}r}{2{v}_{0}}$=$\frac{\sqrt{3}m}{qB}$
粒子从N到P所用的时间:t2=$\frac{120°}{360°}$T=$\frac{1}{3}$×$\frac{2πm}{qB}$=$\frac{2πm}{3qB}$
故总时间 t=t1+t2=$\frac{\sqrt{3}m}{qB}$+$\frac{2πm}{3qB}$.
答:(1)M、N两点间的电势差UMN为$\frac{3m{v}_{0}^{2}}{2q}$.
(3)粒子在磁场中运动的轨道半径r为$\frac{2m{v}_{0}}{qB}$.
(4)粒子从M点运动到P点的总时间t为$\frac{\sqrt{3}m}{qB}$+$\frac{2πm}{3qB}$.
点评 粒子在电场中运动偏转时,常用能量的观点来解决问题,有时也要运用运动的合成与分解.粒子在磁场中做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点,要正确画出粒子运动的轨迹图,能熟练的运用几何知识解决物理问题.

 名校课堂系列答案
名校课堂系列答案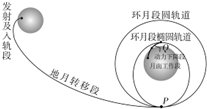 2013年12月2日1时30分,嫦娥三号探测器由长征三号乙运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察.嫦娥三号的飞行轨道示意图如图所示.假设嫦娥三号在环月段圆轨道和椭圆轨道上运动时,只受到月球的万有引力.则以下说法正确的是( )
2013年12月2日1时30分,嫦娥三号探测器由长征三号乙运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察.嫦娥三号的飞行轨道示意图如图所示.假设嫦娥三号在环月段圆轨道和椭圆轨道上运动时,只受到月球的万有引力.则以下说法正确的是( )| A. | 若已知嫦娥三号环月段圆轨道的半径、运动周期和引力常量,则可以计算出月球的密度 | |
| B. | 嫦娥三号由环月段圆轨道变轨进入环月段椭圆轨道时,应让发动机点火使其加速 | |
| C. | 嫦娥三号在动力下降阶段,其动能增加 | |
| D. | 嫦娥三号在环月段椭圆轨道上P点的速度大于Q点的速度 |
 一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )
一质点,从t=0开始从原点以初速度为0出发,沿X轴运动,其v-t图如图所示,则以下说法正确的是( )| A. | t=0.5s时离原点最远 | B. | t=1s时离原点最远 | ||
| C. | t=1s时回到原点 | D. | t=2s时回到原点 |
| A. | 根据I=$\frac{q}{t}$,可知I与q成正比 | |
| B. | 将导体放置于匀强电场中,导体中就会有恒定的电流 | |
| C. | 规定正电荷定向移动的方向为电流的方向,电流是矢量 | |
| D. | 电流的单位“安培”是国际单位制中的基本单位 |

(1)请将图2中的实物连线按电路图补充完整.
(2)考虑电表内阻的影响,该元件电阻的测量值小于(选填“大于”、“等于”或“小于”)真实值.
(3)在电路图中闭合开关S,电流表、电压表均有示数,但无论怎样移动变阻器滑动片,总不能使电压表的示数调为零.原因可能是图中的f(选填a、b、c、d、e、f)处接触不良.
(4)实验测得表格中的7组数据.请在图3坐标纸上作出该元件的I-U图线.
| 序号 | 电压/V | 电流/A |
| 1 | 0.00 | 0.00 |
| 2 | 0.40 | 0.02 |
| 3 | 0.80 | 0.05 |
| 4 | 1.20 | 0.12 |
| 5 | 1.60 | 0.20 |
| 6 | 2.00 | 0.31 |
| 7 | 2.40 | 0.44 |





