题目内容
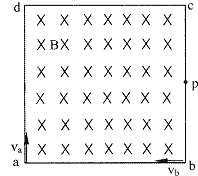 如图所示,正方形区域内有垂直于纸面向里的匀强磁场,磁感应强度为B,两个电子分别从a、b两点沿图示方向射人磁场且恰好在bc边的中点p处相遇,不计两电子间的作用力,不计重力,电子的比荷(
如图所示,正方形区域内有垂直于纸面向里的匀强磁场,磁感应强度为B,两个电子分别从a、b两点沿图示方向射人磁场且恰好在bc边的中点p处相遇,不计两电子间的作用力,不计重力,电子的比荷(| e |
| m |
(1)两电子速率之比
| νa |
| νb |
(2)两电子进入磁场的时间差△t.
分析:(1)两个电子进入磁场中都做匀速圆周运动,运用几何方法画出轨迹,由几何知识求出两个电子轨迹半径,可由牛顿第二定律和向心力列式,求得速率之比;
(2)两个电子运动周期相同.根据轨迹,得出轨迹所对的圆心角,得到运动时间与周期的关系,即可求出时间差.
(2)两个电子运动周期相同.根据轨迹,得出轨迹所对的圆心角,得到运动时间与周期的关系,即可求出时间差.
解答:解:(1)如图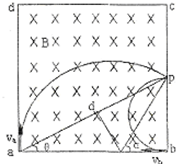 ,设磁场区域半径为L,rb=
,设磁场区域半径为L,rb=
…①
由几何知识得
L2+(
)2=d2,cosθ=
,cosθ=
解得:ra=
L…②
据牛顿第二定律 qvB=
…③
得:v=
则得
=
=
…④
(2)两电子圆周运动的周期相同,都为 T=
=
=
…⑤
如图sina=
=
ta=
T=
(π-arcsin
)…⑥
tb=
T
…⑦
△t=tb-ta=
arcsin
…⑧
答:
(1)两电子速率之比
为
.
(2)两电子进入磁场的时间差△t为
arcsin
.
 ,设磁场区域半径为L,rb=
,设磁场区域半径为L,rb=| L |
| 4 |
由几何知识得
L2+(
| L |
| 2 |
| L |
| d |
| ||
| ra |
解得:ra=
| 5 |
| 8 |
据牛顿第二定律 qvB=
| mv2 |
| r |
得:v=
| qBr |
| m |
则得
| va |
| vb |
| ra |
| rb |
| 5 |
| 2 |
(2)两电子圆周运动的周期相同,都为 T=
| 2πr |
| v |
| 2πm |
| Bq |
| 2π |
| kB |
如图sina=
| ||
| ra |
| 4 |
| 5 |
| π-a |
| 2π |
| 1 |
| kB |
| 4 |
| 5 |
tb=
| 1 |
| 2 |
| π |
| kB |
△t=tb-ta=
| 1 |
| kB |
| 4 |
| 5 |
答:
(1)两电子速率之比
| νa |
| νb |
| 5 |
| 2 |
(2)两电子进入磁场的时间差△t为
| 1 |
| kB |
| 4 |
| 5 |
点评:本题考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,同时还要注意几何关系的运用.

练习册系列答案
相关题目
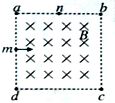 如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里.一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场.现将磁场的磁感应强度变为原来的2倍,其他条件不变,则下列判断正确的是( )
如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里.一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场.现将磁场的磁感应强度变为原来的2倍,其他条件不变,则下列判断正确的是( )| A、粒子将从a点射出磁场 | B、粒子将从b射出磁场 | C、粒子在磁场中运动的时间相同 | D、粒子在磁场中运动的时间不同 |

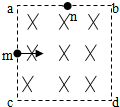 如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里,一个氢核从ac边的中点m沿着既垂直于ac边又垂直磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场,若将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核射出磁场的位置是
如图所示,正方形区域abcd中充满匀强磁场,磁场方向垂直纸面向里,一个氢核从ac边的中点m沿着既垂直于ac边又垂直磁场的方向,以一定速度射入磁场,正好从ab边中点n射出磁场,若将磁场的磁感应强度变为原来的2倍,其他条件不变,则这个氢核射出磁场的位置是 如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场.在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点.下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )
如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场.在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点.下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )