��Ŀ����
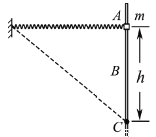
����Ŀ����ͼ��ʾ����ֱƽ���ڷ�һֱ��Բ��AOB��ˮƽ����ֱ�ĸ��ϸ���������Ϊm��С��A��B�������棨�����Ŀ���Բ��ֱ����Щ����A��B���ò����쳤������Ϊl��������������֪��ֱ�˹⻬��ˮƽ�˴ֲڣ���������ֱ�˼�ļн�Ϊ�ȣ�����=37��ʱA��ǡ�þ�ֹ������һˮƽ��F������A��ʹA�����˶�����=53�㴦�������Ħ�������ڻ���Ħ�������������ٶ�Ϊg��sin37��=0.6��cos37��=0.8���� ��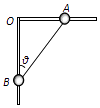
A.A������ֱ�˼�Ķ�Ħ������Ϊ0.375
B.A���˶����̣���������Ϊ1.2mg
C.��һ����A��˷�Ħ�������Ĺ�Ϊ0.15mgl
D.ˮƽ��F���Ĺ�Ϊ0.32 mgl
���𰸡�A,C
���������⣺A������=37��ʱA��ǡ�þ�ֹ��B��Ϊ�о������������������ͼ1��ʾ������ƽ�������ã�
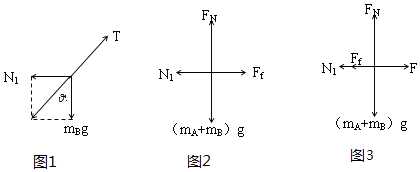
N1=mgtan��
�������о�������������ͼ2��ʾ����ƽ�������ã�
FN=��mA+mB��g=2mg
N1=Ff
�� Ff=��N1
�����ã�2��mg=mgtan��
���A������ֱ�˼�Ķ�Ħ������Ϊ����=0.375����A��ȷ��
B����A��Ҫ������ʱ���������ͼ3��ʾ�����У�F=N1+Ff=mgtan��+2��mg=1.5mg������A���˶����̣���������Ϊ1.5mg����B����
C����ͼ3֪����С��A���һ����ƶ�ʱ��FN���䣬����Ff=��FN��Ff���䣮���У�Ff=2��mg=0.75mg
A�����˶�����=53�㴦ʱ�ƶ��ľ���Ϊ x=lsin53�㩁lsin37��=0.2l��������һ����A��˷�Ħ�������Ĺ�Ϊ WFf=Ffx=0.15mgl����C��ȷ��
D����AB���壬�ɶ��ܶ����ã�WF��WFf��mg��lcos37�㩁lcos53�㣩=0�����ˮƽ��F���Ĺ�Ϊ WF=0.35mgl����D����
��ѡ��AC
�����㾫�������ù��ܹ�ϵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�