题目内容
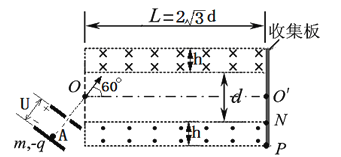
【题目】某装置用磁场控制带电粒子的运动,工作原理图如图所示。装置的长L=![]() ,上下两个相同的矩形区域内存在匀强磁场,磁感应强度大小相同、方向与纸面垂直且相反,两磁场的间距为d,装置右端有一收集板,N、P为板上的两点,N、P分别位于下方磁场的上、下边界上。一质量为m、电荷量为-q的粒子静止在A处,经加速电场加速后,以速度v0沿图中的虚线从装置左端的中点O射入,方向与轴线成60°角。可以通过改变上下矩形区域内的磁场强弱(两磁场始终大小相同、方向相反),控制粒子到达收集板上的位置。不计粒子的重力。
,上下两个相同的矩形区域内存在匀强磁场,磁感应强度大小相同、方向与纸面垂直且相反,两磁场的间距为d,装置右端有一收集板,N、P为板上的两点,N、P分别位于下方磁场的上、下边界上。一质量为m、电荷量为-q的粒子静止在A处,经加速电场加速后,以速度v0沿图中的虚线从装置左端的中点O射入,方向与轴线成60°角。可以通过改变上下矩形区域内的磁场强弱(两磁场始终大小相同、方向相反),控制粒子到达收集板上的位置。不计粒子的重力。
(1)试求出加速电压U的大小;
(2)若粒子只经过上方的磁场区域一次,恰好到达收集板上的P点,求磁场区域的宽度h;
(3)欲使粒子经过上下两磁场并到达收集板上的N点,磁感应强度有多个可能的值,试求出其中的最小值B。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)由动能定理可知: ![]()
得: ![]() 。
。
(2)设带电粒子在磁场中运动的轨道半径为r,依题意作出带电粒子的运动轨迹如下图所示。由图中几何关系有: 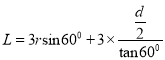 ,
,
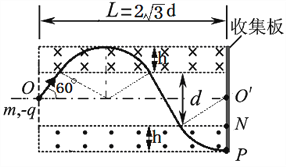
![]()
解得: ![]()
(3)当B为最小值时,粒子运动的轨道半径r则为最大值,即粒子只经过上方和下方的磁场区域各一次,恰好到达收集板上的N点。设带电粒子此时运动的轨道半径为![]() ,带电粒子的运动轨迹如下图所示。
,带电粒子的运动轨迹如下图所示。
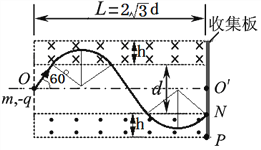
由图中几何关系有: 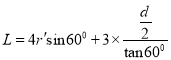
根据牛顿第二定律和洛伦兹力大小公式有: ![]()
联立以上各式解得: ![]() 。
。

【题目】一辆电动自行车的铭牌上给出了如下的技术参数表
规格 | 后轮驱动直流永磁毂电机 | |||
车型 | 26″电动自行车 | 额定输出功率 | 120W | |
整车质量 | 30kg | 额定电压 | 40V | |
最大载重 | 120kg | 额定电流 | 3.5A | |
质量为M=70kg的人骑此电动自行车沿平直公路行驶,所受阻力f恒为车和人总重的k=0.20倍。取g=10m/s2,求:
(1)此车永磁毂电机在额定电压下正常工作的效率。
(2)仅在永磁毂电机以额定功率提供动力的情况下,人骑车行驶的最大速度。
(3)仅在永磁毂电机以额定功率提供动力的情况下,当车速为v1=1.0m/s时,人骑车的最大加速度。

