题目内容
【题目】如图所示，水平向右的匀强电场中，用长为L的绝缘轻质细绳悬桂一小球，O为悬点。小球质量为m，带电量为+ q。将小球拉至悬点O的正下方A位置无初速度释放，小球将向右摆动，细绳向右偏离竖直方向的最大偏角
=60%重力加速度为g，不计一切阻力。
（1）求该匀强电场强度E的大小；
（2）将小球向右拉至与O等髙的B位置，细绳拉直，小球由静止释放，求在小球摆动过程中，细绳所受的最大拉力和小球向左运动到达位置与B位置电势差的最大值。
【答案】（1）
（2）
；
【解析】
（1）在小球由A位置释放到向右摆到最大偏角
的过程中，由动能定理得：
qELsin-mgL（1-cos）= 0
解得：
E=；
（2）
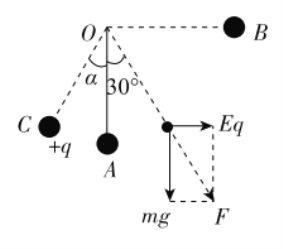
由于：
=tan 30°，
则小球所受电场力与重力的合力F的方向与OA方向成30°，此位置细绳所受的拉力最大为T，由动能定理和牛顿第二定律得：
mgLcos30°-qEL（1-sin 30°）=
T-
解得：
T=
要使小球向左运动到达位置与B位置电势差最大，则小球向左运动的位置C距B的水平距离最大，设OC与OA夹角为α，由动能定理得：
mgLcosα-qEL（ 1 + sinα）=0
整理得：
由三角公式知：
得：
=30°，
即 α= 30°
所求电势差的最大值为：
UCB= EL（1+sinα）=
练习册系列答案
阅读快车系列答案
相关题目
