题目内容
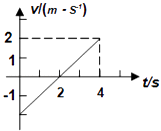
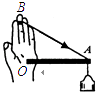
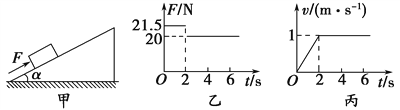
【题目】某同学为了探究物体与斜面间的动摩擦因数进行了如下实验，取一质量为m的物体使其在沿斜面方向的推力作用下向上运动，如图甲所示，通过力传感器得到推力随时间变化的规律如图乙所示，通过频闪照相处理后得出速度随时间变化的规律如图丙所示，若已知斜面的倾角α＝30°，取重力加速度g＝10 m/s2，则由此可得 ( )．
A. 物体的质量为3 kg
B. 物体与斜面间的动摩擦因数为
C. 撤去推力F后，物体将做匀减速运动，最后可以静止在斜面上
D. 撤去推力F后，物体下滑时的加速度为
m/s2
【答案】ABD
【解析】A、由图丙所示图象可知，0～2s内，物体加速度
，由图乙所示，此段时间内的推力F1=21.5N，由牛顿第二定律得F1-mgsin30°+μmgcos30°=ma ①，由图丙所示可知，2s以后物体做匀速直线运动，由图乙所示图象可知，此时推力F2=20N，由平衡条件得：F2=mgsin30°+μmgcos30°②，由①②解得：m=3kg， 
，故A、B正确；C、物体与斜面间的滑动摩擦力f=μmgcos30°=5N，重力沿斜面向下的分力G1=mgsin30°=15N＞f，则物体速度变为零后要反向向下加速度滑动，不会静止在斜面上，故C错误；D、撤去推力物体下滑时，由牛顿第二定律得：μmgcos30°-mgsin30°=ma， 
，故D正确；故选ABD.
练习册系列答案
相关题目
