题目内容
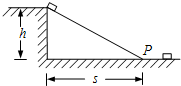
如图所示,一薄木板斜搁在高为h=0.2m的平台和水平地板上,其顶端与平台相平,末端位于地板的P处,并与地板平滑连接,己知P点到平台的水平距离为s=1m.现有一滑块正在木板上以4m/s的速度匀速下滑,g取10/m2,问:
(1)滑块与木板间的动摩擦因数是多大?
(2)若滑块与木板及地板间的动摩擦因数相同,滑块最终将停在何处?
(1)滑块与木板间的动摩擦因数是多大?
(2)若滑块与木板及地板间的动摩擦因数相同,滑块最终将停在何处?

(1)设斜面的倾角为θ,滑块在木板上受力平衡
mgsinθ=μFN
mgcosθ=FN
联立并代入数据解得μ=tanθ=
=0.2.
(2)滑块进入水平地板后做匀减速运动,根据牛顿第二定律得,
μmg=ma
解得a=μg=2m/s2
再根据vt2-v02=-2ax
解得x=
=4m
故滑块最终停在距P点右边4m的水平地板上.
答:(1)滑块与木板间的动摩擦因数是0.2.
(2)滑块最终停在距P点右边4m的水平地板上.
mgsinθ=μFN
mgcosθ=FN
联立并代入数据解得μ=tanθ=
| h |
| s |
(2)滑块进入水平地板后做匀减速运动,根据牛顿第二定律得,
μmg=ma
解得a=μg=2m/s2
再根据vt2-v02=-2ax
解得x=
| vt2-v02 |
| -2a |
故滑块最终停在距P点右边4m的水平地板上.
答:(1)滑块与木板间的动摩擦因数是0.2.
(2)滑块最终停在距P点右边4m的水平地板上.

练习册系列答案
相关题目