题目内容
3. 用图示装置测量重锤的质量,在定滑轮两侧分别挂上重锤和n块质量均为m0的铁片,重锤下端贴一遮光片,铁架台上安装有光电门.调整重锤的高度,使其从适当的位置由静止开始下落,读出遮光片通过光电门的挡光时间t0;从定滑轮左侧依次取下1块铁片放到右侧重锤上,让重锤每次都从同一位置由静止开始下落,计时器记录的挡光时间分别为t1、t2…,计算出t02、t12….
用图示装置测量重锤的质量,在定滑轮两侧分别挂上重锤和n块质量均为m0的铁片,重锤下端贴一遮光片,铁架台上安装有光电门.调整重锤的高度,使其从适当的位置由静止开始下落,读出遮光片通过光电门的挡光时间t0;从定滑轮左侧依次取下1块铁片放到右侧重锤上,让重锤每次都从同一位置由静止开始下落,计时器记录的挡光时间分别为t1、t2…,计算出t02、t12….(1)挡光时间为t0时,重锤的加速度为a0.从左侧取下i块铁片置于右侧重锤上时,对应的挡光时间为ti,重锤的加速度为ai.则$\frac{{a}_{i}}{{a}_{0}}$=$\frac{t_0^2}{t_i^2}$.(结果用t0和ti表示)
(2)作出$\frac{{a}_{i}}{{a}_{0}}$-i的图线是一条直线,直线的斜率为k,则重锤的质量M=$\frac{2+nk}{k}{m_0}$.
(3)若重锤的质量约为300g,为使实验测量数据合理,铁片质量m0比较恰当的取值是C.
A.1g B.5g C.40g D.100g.
分析 (1)当时间较短时,可以用平均速度代替瞬时速度,求出重锤到达光电门的速度,再根据匀加速直线运动位移速度公式联立方程求解;
(2)根据牛顿第二定律表示出$\frac{a_i}{a_0}$-i的函数关系,根据斜率为k求解;
(3)为了使重锤的加速度不至于太大,或把铁片取下放到重锤上时,加速度产生明显的变化的原则选择铁片的质量;
解答 解:(1)设挡光条的宽度为d,则重锤到达光电门的速度v=$\frac{d}{t}$,
当挡光时间为t0时的速度${v}_{0}=\frac{d}{{t}_{0}}$①,
挡光时间为ti时的速度${v}_{i}=\frac{d}{{t}_{i}}$②,
重锤在竖直方向做匀加速直线运动,则有:
2${a}_{0}h={{v}_{0}}^{2}$③,
2${a}_{i}h={{v}_{i}}^{2}$④,
由①②③④解得:$\frac{{a}_{i}}{{a}_{0}}$=$\frac{{t}_{0}^{2}}{{t}_{i}^{2}}$
(2)根据牛顿第二定律得:
${a}_{0}=\frac{Mg-n{m}_{0}g}{M}$⑤
${a}_{i}=\frac{Mg+i{m}_{0}g-(n-i){m}_{0}g}{M}$⑥
由⑤⑥解得:$\frac{{a}_{i}}{{a}_{0}}=\frac{2{m}_{0}}{M-n{m}_{0}}i+1$,
作出$\frac{a_i}{a_0}$-i的图线的斜率为k,则
$\frac{2{m}_{0}}{M-n{m}_{0}}$=k
解得:M=$\frac{2+nk}{k}{m}_{0}$
(3)重锤的质量约为300g,为了使重锤的加速度不至于太大,或把铁片取下放到重锤上时,加速度产生明显的变化,则铁片的质量不能太小,也不能太大,所以1g、5g和100g都不适合,故C正确.
故选:C
故答案为:(1)$\frac{t_0^2}{t_i^2}$;(2)$\frac{2+nk}{k}{m_0}$;(3)C;
点评 本实验比较新颖,考查了运动学基本公式就牛顿第二定律的应用,要求同学们知道,当时间较短时,可以用平均速度代替瞬时速度,难度适中.

| A. | 伽利略 | B. | 牛顿 | C. | 亚里士多德 | D. | 卡文迪许 |
| A. | 若A球带正电、C球带负电,将A球沿AB连线缓慢远离B球,则C球也将缓慢离开B球 | |
| B. | 若A球带正电、C球带正电,将A球沿AB连线缓慢靠近B球,则C球也将缓慢靠近B球 | |
| C. | 若三球带同种电荷,将A球带电量突然减小为某一值,C球将一直做加速度越来越小的运动 | |
| D. | 若三球带同种电荷,将C球从平衡位置略微向正上方拉起后静止释放,C球不可能静止 |
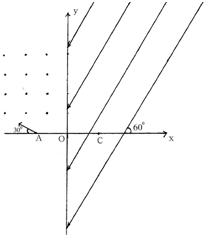 如图所示,第一、四象限内存在一匀强电场,其方向如图所示.第二象限内有垂直纸面向外磁感应强度为B的匀强磁场,一个质量为m,电荷量为+q(不计重力) 的带电粒子从x轴上的A点以初速度v0沿垂直于磁感线方向进入匀强磁场中,初速度方向与x轴负方向的夹角θ=30°粒子恰好从 y轴上的P点垂直于电场线的方向射入匀强电场,经过x轴上的C点再到达 y轴上的D点,已知AO=OC(P、D两点图中未标出 ),
如图所示,第一、四象限内存在一匀强电场,其方向如图所示.第二象限内有垂直纸面向外磁感应强度为B的匀强磁场,一个质量为m,电荷量为+q(不计重力) 的带电粒子从x轴上的A点以初速度v0沿垂直于磁感线方向进入匀强磁场中,初速度方向与x轴负方向的夹角θ=30°粒子恰好从 y轴上的P点垂直于电场线的方向射入匀强电场,经过x轴上的C点再到达 y轴上的D点,已知AO=OC(P、D两点图中未标出 ),
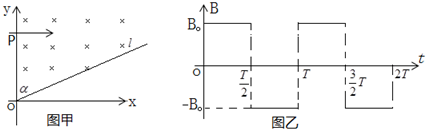
 如图所示,质量mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以初速度v0=10m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为1m/s、4m/s.求:
如图所示,质量mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B以初速度v0=10m/s沿水平方向向右运动,与A碰撞后都向右运动.木块A与挡板碰撞后立即反弹(设木块A与挡板碰撞过程无机械能损失).后来木块A与B发生二次碰撞,碰后A、B同向运动,速度大小分别为1m/s、4m/s.求: 如图所示,竖直固定的足够长的光滑金属导轨MN、PQ,间距为l=0.2m,其电阻不计.完全相同的两金属棒ab、cd垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.01kg,电阻均为R=0.2Ω,棒cd放置在水平绝缘平台上,整个装置处在垂直于导轨平面向里的匀强磁场中,磁感应强度B=1.0T.棒ab在竖直向上的恒力F作用下由静止开始向上运动,当ab棒运动x=0.1m时达到最大速度vm,此时cd棒对绝缘平台的压力恰好为零.取g=10m/s2,求:
如图所示,竖直固定的足够长的光滑金属导轨MN、PQ,间距为l=0.2m,其电阻不计.完全相同的两金属棒ab、cd垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.01kg,电阻均为R=0.2Ω,棒cd放置在水平绝缘平台上,整个装置处在垂直于导轨平面向里的匀强磁场中,磁感应强度B=1.0T.棒ab在竖直向上的恒力F作用下由静止开始向上运动,当ab棒运动x=0.1m时达到最大速度vm,此时cd棒对绝缘平台的压力恰好为零.取g=10m/s2,求: