Question

如图所示，小圆环A系着一个质量为m₂的物块并套在另一个竖直放置的大圆环上，有一细线一端拴在小圆环A上，另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m₁的物块．如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计，绳子又不可伸长，若平衡时弦AB所对应的圆心角为α，则两物块的质量比m₁：m₂应为（　　）

• A、cos

  a

  2

• B、sin

  a

  2

• C、2sin

  a

  2

• D、2cos

  a

  2

Answer 1

分析：选取小圆环A为研究对象，画受力分析示意图，小圆环受三个力，两个绳子的拉力和大圆环的支持力，一定要知道大圆环的支持力只能是沿着半径的，由此两端绳子拉力分别在切线方向上的分力必然相等，然后由数学三角函数知识求解．

解答：解：如图

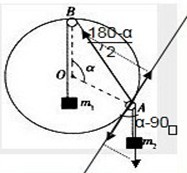
对小环进行受力分析，如图所示，小环受上面绳子的拉力m₁g，下面绳子的拉力m₂g，以及圆环对它沿着OA向外的支持力，将两个绳子的拉力进行正交分解，它们在切线方向的分力应该相等：
m₁gsin

180-α

2

=m₂gcos（α-90）
即：m₁cos

α

2

=m₂sinα
m₁cos

α

2

=2m₂sin

α

2

cos

α

2

得：m₁：m₂=2sin

α

2

故选：C．

点评：本题主要考查了正交分解的方法，另外要重视数学知识在物理中的应用．