题目内容
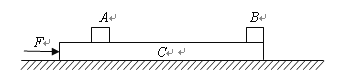
【题目】如图所示，光滑水平面上静止放置质量M = 2kg，长L = 0.84m的长木板C；离板左端S = 0.12m处静止放置质量mA =1kg的小物块A，A与C间的动摩擦因数μ = 0.4；在板右端静止放置质量mB = 1kg的小物块B，B与C间的摩擦忽略不计．设最大静摩擦力等于滑动摩擦力，A、B均可视为质点，g = 10m/s2．现在木板上加一水平向右的力F，问：
（1）当F = 9N时，小物块A的加速度为多大？
（2）若F足够大，则A与B碰撞之前运动的最短时间是多少？
（3）若在A与B发生弹性碰撞时撤去力F，A最终能滑出C，则F的取值范围是多少？
【答案】（1）3 m/s2 （2）0.6s （3）
【解析】试题分析：（1）设M和mA一起向右加速，它们之间静摩擦力为f
由牛顿第二定律得：F=(M+mA)a------------------------------2分
得：
----------------------------------------------------------2分
，表明加速度的结果是正确的．（1分）
（2）mA在与mB碰之前运动时间最短，必须加速度最大，则：
--------------------------------------------2分
---------------------------------------------1分
解得：
-----------------------------------------1分
（3）在A与B发生碰撞时，A刚好滑至板的左端，则此种情况推力最大，设为F1，
对板Ｃ，有：
---------------------------------------1分
----------------------------------------------1分
解得：
----------------------------------------------1分
若A与C没有发生相对滑动，设推力最小为F2．A与B发生弹性碰撞之前，
对A和C，有：
-----------------------1分
A与B发生弹性碰撞，因质量相等，A的速度交换给B，A静止------1分
而后刚好撤去外力，A与C发生相对滑动，A滑至C的左端时A、C刚好共速，有：
---------------------------------------------------------1分
-------------------------------１分
解得：
------------------------------------------1分
综合以上分析，推力的范围：--------------------1分
