题目内容
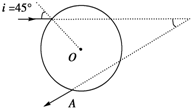 单色细光束射到折射率n=
单色细光束射到折射率n=| 2 |
(1)在图上大致画出光线在球内的路径和方向.
(2)求入射光与出射光之间的夹角α
(3)如果入射光是一束白光,透明球的色散情况与玻璃相仿,问哪种颜色光的α角最大,哪种颜色光的α角最小?
分析:(1)光线从入射到出射的光路如下图所示.入射光线AB经玻璃折射后,折射光线为BC,又经球内壁反射后,反射光线为CD,再经折射后,折射出的光线为DE.OB、OD为球的半球,即为法线.作出光路图.
(2)由折射定律求出折射角r,根据几何知识和对称性求出α.
(3)根据上题的结论,分析α与折射率n的关系,抓住紫光的折射率大于红光的折射率进行分析.
(2)由折射定律求出折射角r,根据几何知识和对称性求出α.
(3)根据上题的结论,分析α与折射率n的关系,抓住紫光的折射率大于红光的折射率进行分析.
解答: 解:(1)光线从入射到出射的光路如下图所示.入射光线AB经玻璃折射后,折射光线为BC,又经球内壁反射后,反射光线为CD,再经折射后,折射出的光线为DE.OB、OD为球的半球,即为法线.
解:(1)光线从入射到出射的光路如下图所示.入射光线AB经玻璃折射后,折射光线为BC,又经球内壁反射后,反射光线为CD,再经折射后,折射出的光线为DE.OB、OD为球的半球,即为法线.
(2)由折射定律
=n,得sinr=
=
=
∴r=30°
由几何关系及对称性,有
=r-(i-r)=2r-i
∴α=4r-2i,把r=30°,i=45°代入得α=30°
(3)由(2)问解答可知,i=45°,n越小,sinr越大,r角越大,同时α=2r-i.
∴红光的α最大,紫光的α最小.
答:
(1)如图所示.
(2)入射光与出射光之间的夹角α为30°;
(3)红光的α最大,紫光的α最小.
 解:(1)光线从入射到出射的光路如下图所示.入射光线AB经玻璃折射后,折射光线为BC,又经球内壁反射后,反射光线为CD,再经折射后,折射出的光线为DE.OB、OD为球的半球,即为法线.
解:(1)光线从入射到出射的光路如下图所示.入射光线AB经玻璃折射后,折射光线为BC,又经球内壁反射后,反射光线为CD,再经折射后,折射出的光线为DE.OB、OD为球的半球,即为法线.(2)由折射定律
| sini |
| sinr |
| sini |
| n |
| ||
|
| 1 |
| 2 |
∴r=30°
由几何关系及对称性,有
| α |
| 2 |
∴α=4r-2i,把r=30°,i=45°代入得α=30°
(3)由(2)问解答可知,i=45°,n越小,sinr越大,r角越大,同时α=2r-i.
∴红光的α最大,紫光的α最小.
答:
(1)如图所示.
(2)入射光与出射光之间的夹角α为30°;
(3)红光的α最大,紫光的α最小.
点评:本题是几何光学问题,作出光路图是解题的基础,同时要善于运用几何关系分析光线的偏折角与折射角和入射角的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 单色细光束射到折射率
单色细光束射到折射率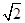 的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).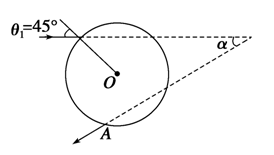
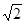 的透明球表面,光束在过球心的平面内,入射角i=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角i=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(已画出入射光线和出射光线).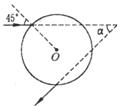
 (3)如果入射的是一束白光,透明球的色散情况与玻璃球相仿,问哪种颜色光的α角最大,哪种颜色光的α角最小?
(3)如果入射的是一束白光,透明球的色散情况与玻璃球相仿,问哪种颜色光的α角最大,哪种颜色光的α角最小?