题目内容
13. 如图所示,光滑的水平面AB与半径R=0.4m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点,A点的右侧连接一粗糙的水平面.用细线连接甲、乙两物体,中问夹一轻质压缩弹簧,弹簧与甲、乙两物体不拴接,甲的质量朋m1=4kg,乙的质量m2=5kg,甲、乙均静止.若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零.取g=10m/s2,甲、乙两物体均可看作质点,求:
如图所示,光滑的水平面AB与半径R=0.4m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点,A点的右侧连接一粗糙的水平面.用细线连接甲、乙两物体,中问夹一轻质压缩弹簧,弹簧与甲、乙两物体不拴接,甲的质量朋m1=4kg,乙的质量m2=5kg,甲、乙均静止.若固定乙,烧断细线,甲离开弹簧后经过B点进入半圆轨道,过D点时对轨道的压力恰好为零.取g=10m/s2,甲、乙两物体均可看作质点,求:(1)甲离开弹簧后经过B点时的速度的大小vB;
(2)在弹簧压缩量相同的情况下,若固定甲,烧断细线,乙物体离开弹簧后从A点进入动摩擦因数μ=0.4的粗糙水平面,则乙物体在粗糙水平面运动的位移S.
分析 (1)根据牛顿第二定律求出甲在D点的速度,根据机械能守恒定律求出甲离开弹簧后经过B点的速度大小.
(2)根据能量守恒求出乙的初速度,结合牛顿第二定律和速度位移公式求出物体在粗糙水平面上运动的位移大小.
解答 解:(1)甲在最高点D,由牛顿第二定律得:m1g=m1$\frac{{v}_{D}^{2}}{R}$,
设甲离开弹簧运动至D点的过程中机械能守恒,由机械能守恒定律得:
$\frac{1}{2}$m1vB2=$\frac{1}{2}$m1vD2+m1g•2R,
代入数据联立解得:vB=2$\sqrt{5}$m/s.
(2)甲固定,烧断细线后乙的速度大小为v2,由能量守恒定律得:
EP=$\frac{1}{2}$m1vB2=$\frac{1}{2}$m2v22,
代入数据解得:v2=4m/s.
乙在粗糙水平面做匀减速运动:μm2g=m2a,
代入数据解得:a=4m/s2,
则有:s=$\frac{{v}_{2}^{2}}{2a}$=$\frac{{4}^{2}}{2×4}$=2m.
答:(1)甲离开弹簧后经过B点时的速度的大小为2$\sqrt{5}$m/s;
(2)乙物体在粗糙水平面运动的位移为2m.
点评 本题考查了牛顿第二定律、机械能守恒定律、能量守恒定律和运动学公式的综合运用,关键理清甲乙的运动规律,选择合适的规律进行求解.注意弹簧压缩量相同时,弹性势能相等.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 牛顿发现了万有引力定律,并测出了引力常量 | |
| B. | 安培发现了电流的磁效应,洛伦兹通过实验测定了磁场对电流的作用力 | |
| C. | 静止导线中通稳恒电流也可以在近旁的静止线圈中感应出电流 | |
| D. | 伽利略科学思想的核心是把科学实验和逻辑推理有机结合起来 |
1.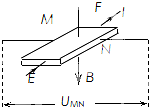 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )| A. | 霍尔元件能够把电学量转换为磁学量的传感器 | |
| B. | 若霍尔元件的载流子是自由电子,则电势差UMN<0 | |
| C. | 仅增大磁感应强度时,电势差UMN变大 | |
| D. | 在测定地球赤道上方的地磁场强弱时,元件的工作面应保持水平 |
8.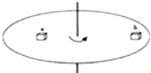 如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
 如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )| A. | 1:1 | B. | 3:2 | C. | 2:3 | D. | 9:4 |
18.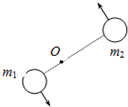 两个靠近的天体称为双星,它们以两者连线上某点O为圆心做匀速圆周运动,其质量分别为m1、m2,如图所示,以下说法正确的是( )
两个靠近的天体称为双星,它们以两者连线上某点O为圆心做匀速圆周运动,其质量分别为m1、m2,如图所示,以下说法正确的是( )
 两个靠近的天体称为双星,它们以两者连线上某点O为圆心做匀速圆周运动,其质量分别为m1、m2,如图所示,以下说法正确的是( )
两个靠近的天体称为双星,它们以两者连线上某点O为圆心做匀速圆周运动,其质量分别为m1、m2,如图所示,以下说法正确的是( )| A. | 它们的角速度相同 | B. | 它们的线速度大小相等 | ||
| C. | 向心力恒定且与质量的乘积成正比 | D. | 轨道半径与质量成反比 |
2. 如图所示,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板上,随跳板一同向下做变速运动到达最低点,然后随跳板反弹,则下列说法中正确的是( )
如图所示,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板上,随跳板一同向下做变速运动到达最低点,然后随跳板反弹,则下列说法中正确的是( )
 如图所示,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板上,随跳板一同向下做变速运动到达最低点,然后随跳板反弹,则下列说法中正确的是( )
如图所示,跳水运动员最后踏板的过程可以简化为下述模型:运动员从高处落到处于自然状态的跳板上,随跳板一同向下做变速运动到达最低点,然后随跳板反弹,则下列说法中正确的是( )| A. | 运动员与跳板接触的全过程中只有超重状态,没有失重状态 | |
| B. | 运动员把跳板压到最低点时,她所受外力的合力不为零 | |
| C. | 运动员能跳得高的原因之一,是因为跳板对她的作用力远大于她的重力 | |
| D. | 运动员能跳得高的原因之一,是因为跳板对她的作用力远大于她对跳板的作用力 |
3. 民航飞机配备的应急逃生滑梯可供乘客在发生紧急事件时从飞机滑行到地面,如图所示.若将滑梯视为斜面,乘客在滑梯上的运动看作是匀加速直线运动,则( )
民航飞机配备的应急逃生滑梯可供乘客在发生紧急事件时从飞机滑行到地面,如图所示.若将滑梯视为斜面,乘客在滑梯上的运动看作是匀加速直线运动,则( )
 民航飞机配备的应急逃生滑梯可供乘客在发生紧急事件时从飞机滑行到地面,如图所示.若将滑梯视为斜面,乘客在滑梯上的运动看作是匀加速直线运动,则( )
民航飞机配备的应急逃生滑梯可供乘客在发生紧急事件时从飞机滑行到地面,如图所示.若将滑梯视为斜面,乘客在滑梯上的运动看作是匀加速直线运动,则( )| A. | 乘客在滑梯上滑行时,在相等的时间内速度变化不相等 | |
| B. | 令滑梯与水平地面夹角为θ,则乘客与滑梯的动摩擦因数μ=tanθ | |
| C. | 乘客在滑行至滑梯末端时,双脚蹬地让自己减速并停下,此过程中,脚对地面的作用力等于地面对脚的作用力 | |
| D. | 乘客滑行至滑梯末端停下时,他(她)的惯性也就消失了 |
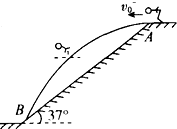 2011年4月,在伦敦举行的国际奥委会执委会上确认,女子跳台滑雪等6个新项目加入2014年冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(末画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20m/s,落点在斜坡L的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10m/s2,sin 37°=0.6,cos37°=0.8)求:
2011年4月,在伦敦举行的国际奥委会执委会上确认,女子跳台滑雪等6个新项目加入2014年冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(末画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20m/s,落点在斜坡L的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10m/s2,sin 37°=0.6,cos37°=0.8)求: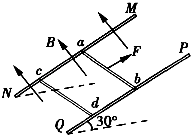 如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问:
如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问: