题目内容
19.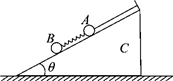 如图所示,一倾角为θ的斜面体C始终静止在水平地面上,它的底面粗糙,斜面光滑.细线的一端系在斜面体顶端的立柱上,另一端与A球连接,轻质弹簧两端分别与质量相等的A、B两球连接.弹簧、细线均与斜面平行,系统处于静止状态.在细线被烧断的瞬间,下列说法正确的是( )
如图所示,一倾角为θ的斜面体C始终静止在水平地面上,它的底面粗糙,斜面光滑.细线的一端系在斜面体顶端的立柱上,另一端与A球连接,轻质弹簧两端分别与质量相等的A、B两球连接.弹簧、细线均与斜面平行,系统处于静止状态.在细线被烧断的瞬间,下列说法正确的是( )| A. | 两球的瞬时加速度均沿斜面向下,大小均为gsinθ | |
| B. | 球A的瞬时加速度沿斜面向下,大小为2gsinθ | |
| C. | 斜面体C对地面的压力等于A、B和C的重力之和 | |
| D. | 地面对斜面体C无摩擦力 |
分析 根据共点力平衡求出烧断细线前弹簧的弹力,烧断细线后,弹簧的弹力不变,结合牛顿第二定律求出A、B的瞬时加速度.烧断细线后,将A的加速度分解为水平方向和竖直方向,运用整体法分析地面的支持力和摩擦力.
解答 解:A、烧断细线前,弹簧的弹力F弹=mgsinθ,烧断细线的瞬间,弹簧的弹力不变,对A,加速度大小${a}_{A}=\frac{{F}_{弹}+mgsinθ}{m}=2gsinθ$,对B,加速度${a}_{B}=\frac{mgsinθ-{F}_{弹}}{m}=0$,故A错误,B正确.
C、烧断细线的瞬间,A的加速度方向沿斜面向下,将A的加速度分解为水平方向和竖直方向,对整体分析可知,斜面体对地面的压力小于A、B和C的重力之和,故C错误.
D、烧断细线的瞬间,A的加速度方向沿斜面向下,在水平方向上有加速度,对整体分析,地面对斜面体的摩擦力不为零,故D错误.
故选:B.
点评 本题考查了牛顿第二定律的瞬时问题,抓住烧断细线的瞬间,弹簧的弹力不变,结合牛顿第二定律求出瞬时加速度.对于分析地面的支持力和摩擦力问题,可以采用整体法研究比较简捷.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
9.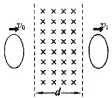 如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )
如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )
 如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )
如图所示,宽度为d的有界匀强磁场竖直向下穿过光滑的水平桌面,一质量为m的椭圆形导体框平放在桌面上,椭圆的长轴平行磁场边界,短轴小于d.现给导体框一个初速度v0(v0垂直磁场边界),已知导体框全部在磁场中的速度为v,导体框全部出磁场后的速度为v1:导体框进入磁场过程中产生的焦耳热为Ql 导体框离开磁场过程中产生的焦耳热为Q2,下列说法正确的是( )| A. | 导体框离开磁场过程中,读者看到的感应电流的方向为顺时针方向 | |
| B. | 导体框进出磁场都是做匀变速直线运动 | |
| C. | Q1=Q2 | |
| D. | Q1+Q2=$\frac{1}{2}$m(v02-v12) |
7. 如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
 如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )
如图所示,水平传送带以速度v1匀速运动,小物体P、Q由通过光滑定滑轮的不可伸长的轻绳相连,t=0时刻P在传送带左端具有速度v2,己知v1>v2,P与定滑轮间的绳水平.不计定滑轮质量,绳足够长,物体与传送带之间的最大静摩擦力和滑动摩擦力相等.从最初直到物体P从传送带离开的过程,以下判断正确的是( )| A. | 物体P可能先减速后加速 | B. | 物体P可能先加速后减速 | ||
| C. | 物体P可能先加速后匀速 | D. | 物体P可能先减速后匀速 |
14.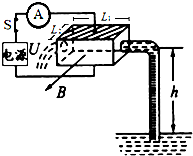 如图为某种电磁泵模型,泵体是长为L1,宽与高均为L2的长方体.泵体处在方向垂直向外、磁感应强度为B的匀强磁场中,泵体的上下表面接电压为U的电源(内阻不计),理想电流表示数为I,若电磁泵和水面高度差为h,液体的电阻率为ρ,在t时间内抽取液体的质量为m,不计液体在流动中和管壁之间的阻力,取重力加速度为g.则( )
如图为某种电磁泵模型,泵体是长为L1,宽与高均为L2的长方体.泵体处在方向垂直向外、磁感应强度为B的匀强磁场中,泵体的上下表面接电压为U的电源(内阻不计),理想电流表示数为I,若电磁泵和水面高度差为h,液体的电阻率为ρ,在t时间内抽取液体的质量为m,不计液体在流动中和管壁之间的阻力,取重力加速度为g.则( )
 如图为某种电磁泵模型,泵体是长为L1,宽与高均为L2的长方体.泵体处在方向垂直向外、磁感应强度为B的匀强磁场中,泵体的上下表面接电压为U的电源(内阻不计),理想电流表示数为I,若电磁泵和水面高度差为h,液体的电阻率为ρ,在t时间内抽取液体的质量为m,不计液体在流动中和管壁之间的阻力,取重力加速度为g.则( )
如图为某种电磁泵模型,泵体是长为L1,宽与高均为L2的长方体.泵体处在方向垂直向外、磁感应强度为B的匀强磁场中,泵体的上下表面接电压为U的电源(内阻不计),理想电流表示数为I,若电磁泵和水面高度差为h,液体的电阻率为ρ,在t时间内抽取液体的质量为m,不计液体在流动中和管壁之间的阻力,取重力加速度为g.则( )| A. | 泵体上表面应接电源负极 | |
| B. | 电磁泵对液体产生的推力大小为BIL1 | |
| C. | 电源提供的电功率为$\frac{{U}^{2}{L}_{1}}{ρ}$ | |
| D. | 质量为m的液体离开泵时的动能为UIt-mgh-I2$\frac{ρ}{{L}_{1}}$t |
4.在人类探索热现象的过程中,下列说法符合历史事实的是( )
| A. | 布朗发现悬浮在水中的花粉颗粒做无规则运动 | |
| B. | 焦耳通过实验证实,在改变内能的方式上做功和热传递是等效的 | |
| C. | 许多科学家在研究热现象时发现,功转变为热这一现象是可逆的 | |
| D. | 开尔文指出绝对零度是温度的下限,可以达到 | |
| E. | 克劳修斯在大量研究的基础上提出,热量不能自发地从低温物体传到高温物体 |
11.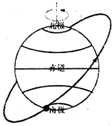 2015年3月30日21时52分,中国在西昌卫星发射中心用长征三号丙运载火箭,成功将首颗新一代北斗导航卫星发射升空.31日凌晨3时34分顺利进入倾斜同步轨道(如图所示,倾斜同步轨道平面与赤道平面有一定夹角),卫星在该轨道的运行周期与地球自转周期相等.此次发射的亮点在于首次在运载火箭上增加了一级独立飞行器为卫星提供动力,可使卫星直接进入轨道,在此之前则是通过圆-椭圆-圆的变轨过程实现.以下说法正确的是( )
2015年3月30日21时52分,中国在西昌卫星发射中心用长征三号丙运载火箭,成功将首颗新一代北斗导航卫星发射升空.31日凌晨3时34分顺利进入倾斜同步轨道(如图所示,倾斜同步轨道平面与赤道平面有一定夹角),卫星在该轨道的运行周期与地球自转周期相等.此次发射的亮点在于首次在运载火箭上增加了一级独立飞行器为卫星提供动力,可使卫星直接进入轨道,在此之前则是通过圆-椭圆-圆的变轨过程实现.以下说法正确的是( )
 2015年3月30日21时52分,中国在西昌卫星发射中心用长征三号丙运载火箭,成功将首颗新一代北斗导航卫星发射升空.31日凌晨3时34分顺利进入倾斜同步轨道(如图所示,倾斜同步轨道平面与赤道平面有一定夹角),卫星在该轨道的运行周期与地球自转周期相等.此次发射的亮点在于首次在运载火箭上增加了一级独立飞行器为卫星提供动力,可使卫星直接进入轨道,在此之前则是通过圆-椭圆-圆的变轨过程实现.以下说法正确的是( )
2015年3月30日21时52分,中国在西昌卫星发射中心用长征三号丙运载火箭,成功将首颗新一代北斗导航卫星发射升空.31日凌晨3时34分顺利进入倾斜同步轨道(如图所示,倾斜同步轨道平面与赤道平面有一定夹角),卫星在该轨道的运行周期与地球自转周期相等.此次发射的亮点在于首次在运载火箭上增加了一级独立飞行器为卫星提供动力,可使卫星直接进入轨道,在此之前则是通过圆-椭圆-圆的变轨过程实现.以下说法正确的是( )| A. | 倾斜同步轨道半径应小于赤道同步轨道半径 | |
| B. | 一级独立飞行器能大大缩短卫星入轨时间 | |
| C. | 倾斜同步卫星加速度的大小等于赤道同步卫星加速度的大小 | |
| D. | 一级独立飞行器携带卫星入轨的过程中,卫星的机械能守恒 |
8.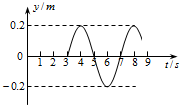 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时起点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m.以下判断正确的是( )| A. | 波源起振方向沿y轴正方向 | B. | 波速大小为0.4m/s | ||
| C. | 波长为1.2m | D. | t=3s时,波源O的动能最大 |
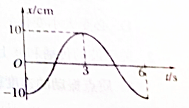 如图所示是某质点做简谐运动的图象,已知质点从t=0时刻开始起振,则由图可知:质点起振后的9s内,通过的路程为0.6m,质点在t=63s末时的位移为0.1m.
如图所示是某质点做简谐运动的图象,已知质点从t=0时刻开始起振,则由图可知:质点起振后的9s内,通过的路程为0.6m,质点在t=63s末时的位移为0.1m.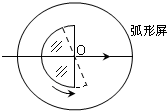 用如图的装置测定玻璃的折射率,半圆形玻璃砖与弧形屏固定,半圆形玻璃砖按图中实线位置放置,使一激光束从玻璃弧面左侧入射并垂直直径平面通过圆心射出玻璃砖,记下入射光束在圆弧形屏上所对应位置的刻度,使玻璃砖以圆心O为轴逆时针缓慢转动,同时观察直径平面一侧出射光线的变化;出射光线不断向下偏转并越来越暗,直到刚好看不到出射光线为止,并记下这时入射光线在弧形屏位置的刻度.这个过程半圆形玻璃砖转过的角度θ就是光束从玻璃射入空气的临界角,玻璃折射率的表达式n=$\frac{1}{sinθ}$.
用如图的装置测定玻璃的折射率,半圆形玻璃砖与弧形屏固定,半圆形玻璃砖按图中实线位置放置,使一激光束从玻璃弧面左侧入射并垂直直径平面通过圆心射出玻璃砖,记下入射光束在圆弧形屏上所对应位置的刻度,使玻璃砖以圆心O为轴逆时针缓慢转动,同时观察直径平面一侧出射光线的变化;出射光线不断向下偏转并越来越暗,直到刚好看不到出射光线为止,并记下这时入射光线在弧形屏位置的刻度.这个过程半圆形玻璃砖转过的角度θ就是光束从玻璃射入空气的临界角,玻璃折射率的表达式n=$\frac{1}{sinθ}$.