题目内容
如图所示，一质量为50Kg的滑块在75N的水平拉力作用下，由静止开始做匀加速直线运动，若滑块与水平地面间的动摩擦因数为O．1，g取lOm/s2．试求：（1）滑块运动的加速度大小；
（2）滑块在前4s的时间内发生的位移的大小．
分析：（1）对木块受力分析，求出合力，再根据牛顿第二定律求加速度；
（2）根据位移时间关系公式求位移．
（2）根据位移时间关系公式求位移．
解答：解：（1）物体受重力、支持力、推力和滑动摩擦力
滑动摩擦力为：f=μmg=0.1×500=50N
根据牛顿第二定律，有
a=
=0.5m/s2
故加速度为0.5m/s2．
（2）由位移时间公式
X=
at2=4m
即滑块在前4s的时间内发生的位移的大小为4m．
滑动摩擦力为：f=μmg=0.1×500=50N
根据牛顿第二定律，有
a=
| F-f |
| m |
故加速度为0.5m/s2．
（2）由位移时间公式
X=
| 1 |
| 2 |
即滑块在前4s的时间内发生的位移的大小为4m．
点评：本题关键受力分析后根据牛顿第二定律求加速度，再根据位移时间关系公式求位移．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，一质量为m=2g，电量为q=5×10-8c的小球，从与水平方向成37°角的两块平行金属板A、B的A板上的小孔P沿水平方向射入，小球在A、B板间做直线运动，两板的间距为d=4cm．问：
如图所示，一质量为M=0.4kg的滑块由光滑弧形凹槽和粗糙水平薄板平滑连接而成，薄板的长度为L=0.3m，厚度忽略不计．将该滑块固定在一高为H=0.8m的光滑水平桌面上，且薄板的右端点与桌子边缘平齐．将一质量为m=0.2kg的小物块（可视为质点）在弧形凹槽上某点由静止释放，小物块落地时距桌面边缘的水平距离为S=0.4m．已知小物块与薄板的动摩擦因数为μ=0.5，空气阻力忽略不计，g取10m/s2．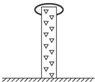
如图所示，一质量为m=1kg、长为L=1m的直棒上附有倒刺，物体顺着直棒倒刺下滑，其阻力只为物体重力的1/5，逆着倒刺而上时，将立即被倒刺卡住．现该直棒直立在地面上静止，一环状弹性环自直棒的顶端由静止开始滑下，设弹性环与地面碰撞不损失机械能，弹性环的质量M=3kg，重力加速度g=10m/s2．求直棒在以后的运动过程中底部离开地面的最大高度．
5.0kg的平板车静止在光滑水平地面上，平板车的上表面距离地面高为
，其右侧足够远处有一障碍物
，另一质量为
kg可视为质点的滑块，以v0=8m/s的初速度从左端滑上平板车，同时对平板车施加一水平向右、大小为5N的恒力
，当滑块运动到平板车的最右端时，二者恰好相对静止，此时撤去恒力
点切入光滑竖直圆弧轨道，并沿轨道下滑，已知滑块与平板车间的动摩擦因数
，圆弧半径为
，圆弧所对的圆心角
=
，取
m/s2，sin53
=0.8，cos53