题目内容
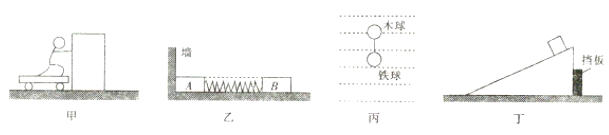
【题目】如图所示，足够长水平光滑轨道连接一半径为R的
光滑圆弧轨道，开始时A球静止，质量为m的球B在水平轨道上以某一初速度向右运动，经过半径为R的光滑圆弧轨道射出。调整挡板位置，发现当B球与固定挡板发生垂直撞击时，撞击点与圆心位置等高，且B球碰撞挡板时没有机械能损失。在物体B碰撞完成返回圆弧轨道后马上撤去挡板，之后B球能与A球在水平轨道上发生不止一次弹性碰撞。则
(1)轨道右端与挡板间的距离x是多少？
(2)B球的初速度v0为多大？
(3)球A的质量M应该满足什么条件？
【答案】(1)
；(2)
；(3)
【解析】
(1)水平方向
轨道最右端
解得
(2)在圆轨道最右端
在圆弧轨道运动过程
解得
(3)两球发生弹性碰撞，要发生多次碰撞则B球一定反向弹回，设碰撞后球B的速度大小为
，碰撞后球A的速度大小为
，
动量守恒
机械能守恒
B球不飞出轨道能返回
返回后球B能追上球A，则有
解得
练习册系列答案
字词句段篇系列答案
相关题目
