题目内容
7. 如图所示,有两根和水平方向成α角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感强度为B,一根质量为m的金属杆从轨道上由静止滑下.经过足够长的时间,金属杆的速度趋近于一个最大速度vm,则( )
如图所示,有两根和水平方向成α角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感强度为B,一根质量为m的金属杆从轨道上由静止滑下.经过足够长的时间,金属杆的速度趋近于一个最大速度vm,则( )| A. | 如果B增大,vm将变大 | B. | 如果α变大,vm将变大 | ||
| C. | 如果R变大,vm将变大 | D. | 如果m变小,vm将变大 |
分析 金属杆受重力、支持力、安培力做加速度逐渐减小的加速运动,当加速度减小到零,速度最大.根据合力为零,求出金属杆的最大的速度.
根据最大的速度的表达式进行求解.
解答 解:金属杆受重力、支持力、安培力,开始时重力沿斜面的分力大于安培力,所以金属杆做加速运动.随着速度的增加,安培力在增大,所以金属杆加速度逐渐减小,当加速度减小到零,速度最大.
当加速度为零时,速度最大.有mgsinα=BIL,
I=$\frac{B{LV}_{m}}{R}$
vm=$\frac{mgsinα•R}{{{B}^{2}L}^{2}}$
A、如果B增大,vm将变小,故A错误.
B、如果α变大,vm将变大,故B正确.
C、如果R变大,vm将变大,故C正确.
D、如果m变小,vm将变小,故D错误.
故选:BC.
点评 解决本题的关键知道金属杆做加速度逐渐减小的加速运动,当加速度为零时,速度最大.

练习册系列答案
相关题目
15.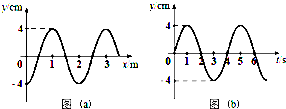 图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=1.5m处的质点的振动图象,P是平衡位置为x=2m的质点.下列说法错误的是( )
图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=1.5m处的质点的振动图象,P是平衡位置为x=2m的质点.下列说法错误的是( )
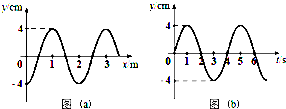 图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=1.5m处的质点的振动图象,P是平衡位置为x=2m的质点.下列说法错误的是( )
图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=1.5m处的质点的振动图象,P是平衡位置为x=2m的质点.下列说法错误的是( )| A. | 波速为0.5m/s | B. | 波的传播方向向右 | ||
| C. | 当t=7s时,P恰好回到平衡位置 | D. | 0~2s时间内,P向y轴负方向运动 |
2.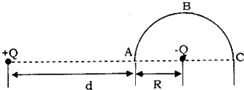 对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d+R,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d+R,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
 对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d+R,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )
对于真空中电荷量为q的静止点电荷而言,当选取离点电荷无穷远处的电势为零时,离点电荷距离为r的位置的电势为φ=$\frac{kq}{r}$(k为静电力常量),如图所示,两电荷量大小均为Q的异种点电荷相距为d+R,现将一质子(电荷量为e)从两电荷连线上的A点沿以负电荷为圆心、半径为R的半圆形轨迹ABC移到C点,在质子从A到C的过程中,系统电势能的变化情况为( )| A. | 减少$\frac{2kQeR}{{d}^{2}-{R}^{2}}$ | B. | 增加$\frac{2kQeR}{{d}^{2}+{R}^{2}}$ | C. | 减少$\frac{2kQeR}{d(d+2R)}$ | D. | 增加$\frac{2kQeR}{d(d+2R)}$ |
12.把两个大小相同的实心铝球和实心铁球放在同一水平面上,它们的重力势能分别为E1和E2.若把它们移至另一个较低的水平面上时,它们的重力势能减少量分别为△E1和△E2则必有( )
| A. | E1<E2 | B. | E1>E2 | C. | △E1<△E2 | D. | △E1<△E2 |
19.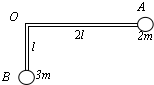 质量不计的直角形支架两端分别连接质量为2m和3m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为2m和3m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
 质量不计的直角形支架两端分别连接质量为2m和3m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为2m和3m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )| A. | A球的最大速度为2$\sqrt{gL}$ | |
| B. | A球的速度最大时,两小球的总重力势能最小 | |
| C. | A球的速度最大时,A杆与竖直方向的夹角为37° | |
| D. | 当B球第一次摆到最高点时,B杆与水平方向的夹角为37° |
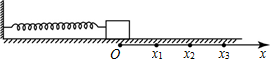 如图所示,弹簧的一端固定,另一端连接一个物块,弹簧质量不计,物块(可视为质点)的质量为m,在水平桌面上沿x轴运动,与桌面间的动摩擦因数为μ,以弹簧原长时物块的位置为坐标原点O,当弹簧的伸长量为x时,物块所受弹簧弹力大小为F=kx,k为常量.
如图所示,弹簧的一端固定,另一端连接一个物块,弹簧质量不计,物块(可视为质点)的质量为m,在水平桌面上沿x轴运动,与桌面间的动摩擦因数为μ,以弹簧原长时物块的位置为坐标原点O,当弹簧的伸长量为x时,物块所受弹簧弹力大小为F=kx,k为常量.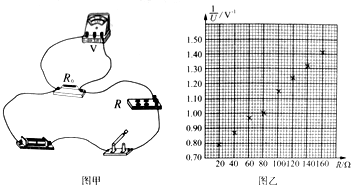
 如图1所示,一列简谐横波沿直线ab向右传播,a、b之间的距离为2m,a、b两点的振动情况如图2所示,则这列波的波长为$\frac{8}{4n+3}$n=0,1,2,…m,波速为$\frac{2}{4n+3}$n=0,1,2,…m/s,这列波的波长可能(选填“可能”或“不可能”)是$\frac{8}{3}$m.
如图1所示,一列简谐横波沿直线ab向右传播,a、b之间的距离为2m,a、b两点的振动情况如图2所示,则这列波的波长为$\frac{8}{4n+3}$n=0,1,2,…m,波速为$\frac{2}{4n+3}$n=0,1,2,…m/s,这列波的波长可能(选填“可能”或“不可能”)是$\frac{8}{3}$m.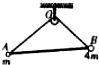 如图所示,两个质量分别为m,4m的质点A、B之间用轻杆连结,并通过长为L的轻绳挂在光滑的定滑轮上,求系统平衡时OA,OB段绳长各为多少.
如图所示,两个质量分别为m,4m的质点A、B之间用轻杆连结,并通过长为L的轻绳挂在光滑的定滑轮上,求系统平衡时OA,OB段绳长各为多少.