题目内容
【题目】某同学参照如图的过山车情景设计了如下模型:弧形轨道的下端与竖直圆轨道相接,使质量为m的小滑块从弧形轨道上端滑下,小滑块从半径为R的圆轨道下端进入后沿圆轨道运动,再滑上与圆轨道圆滑连接的粗糙斜面轨道,与水平面的倾角θ可在0°~75°范围内调节(调节好后即保持不变)。小滑块与斜面间的动摩擦因数![]() ,不计其他轨道和空气阻力。当小滑块恰好能通过圆轨道最高点时,求:
,不计其他轨道和空气阻力。当小滑块恰好能通过圆轨道最高点时,求:

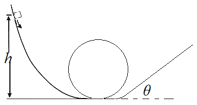
(1)小滑块应从多高处由静止释放;
(2)小滑块经过圆轨道最低点时对轨道的压力大小;
(3)设计的斜面轨道至少多长才能保证小滑块不冲出;并判断该最小长度时,能否保证小滑块不脱离轨道。
【答案】(1)![]() (2)滑块对轨道的压力的大小为6mg
(2)滑块对轨道的压力的大小为6mg
(3)当θ=60°,L最短,在此长度下其他角度均会冲出轨道,此时,![]() 不能保证不脱离轨道
不能保证不脱离轨道
【解析】
(1)滑块恰好到达最高点,即只受重力mg。设滑块经过最高点时的速度为v1,
根据牛顿第二定律可知:![]()
根据动能定理可知:![]()
联立解得:![]() .
.
(2)设滑块经过最低点时的速度为v2
![]()
根据动能定理:![]()
联立解得:F=6mg
根据牛顿第三定律可知,滑块对轨道的压力的大小为6m
(3)设小滑块恰好到达斜面最高点,根据动能定理得:![]()
当θ=60°(满足0°~75°范围),L最短,在此长度下其他角度均会冲出轨道
此时,![]()
因为![]() 所以小滑块要返回,假设速度减为零上升的最大高度为
所以小滑块要返回,假设速度减为零上升的最大高度为![]()
根据动能定理:![]()
解得:![]()
综上,不能保证不脱离轨道

练习册系列答案
相关题目