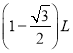题目内容
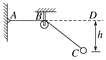
【题目】某实验小组为了探究功与动能变化的关系，利用如图所示的装置.在竖直墙上的A点安装一个拉力传感器，用不可伸长的柔软轻绳一端与质量为1.00 kg的小球C连接，另一端绕过小滑轮B(可以忽略滑轮大小)与传感器连接，定滑轮B与A等高，BD为水平参考线，测出BC间绳长L＝0.80 m.实验中，使绳始终处于绷直状态，将小球从距离BD线高h处由静止开始释放，从拉力传感器记录的拉力变化图线中读出拉力的最大值为F.改变h的值，记录下相应的最大拉力F，取H＝L－h，g＝9.80 m/s2，实验中得到的部分数据如下表所示.
h/m | 0.10 | 0.20 | 0.30 | 0.40 | …… |
H/m | 0.70 | 0.60 | 0.50 | 0.40 | …… |
F/N | 26.88 | 24.45 | 22.00 | 19.56 | …… |
(1)当H＝0.60 m时，小球的最大动能为________ J，此过程中外力做功为________ J；
(2)实验结论是：______________________________________________________
(3)根据实验结论，推导出F与H之间的关系为：__________________.
【答案】 5.86 J 5.88 J 外力所做的功等于物体动能的增量. F＝24.5H＋9.8.
【解析】(1)根据实验中得到的数据可知，H＝0.60 m，F＝24.45 N，
小球运动到最低点时，动能最大，受到的拉力最大，
在最低点，根据牛顿第二定律得：F－mg＝m
解得：
mv2＝5.86 J，
此过程中外力做功为W＝mg(L－h)＝1.00×9.80×0.60 J＝5.88 J.
(2)实验结论为在实验误差允许的范围内，外力所做的功等于物体动能的增量.
(3)根据实验结论可知，F－mg＝m，mv2＝mg(L－h)，解得：F＝
H＋mg，
代入数据得：F＝24.5H＋9.8.
