题目内容
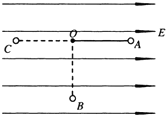 (2011?安徽二模)如图所示,在竖直平面内一个带正电的小球质量为m,所带的电荷量为q用一根长为L且不可伸长的绝缘轻细线系在一匀强电场中的O点.匀强电场的方向水平向右,分布的区域足够大.现将带正电小球从O点右方由水平位置4点无初速度释放,小球到达最低点B时速度恰好为零.
(2011?安徽二模)如图所示,在竖直平面内一个带正电的小球质量为m,所带的电荷量为q用一根长为L且不可伸长的绝缘轻细线系在一匀强电场中的O点.匀强电场的方向水平向右,分布的区域足够大.现将带正电小球从O点右方由水平位置4点无初速度释放,小球到达最低点B时速度恰好为零.(1)求匀强电场的电场强度E的大小.
(2)若小球从O点的左方由水平位置C点无初速度释放,则小球到达最低点B所用的时间t是多少?(已知:
. |
| OA |
. |
| OC |
分析:(1)从A到B小球做变速运动,根据动能定理即可求解,注意电场力和重力做功特点.
(2)当小球从C点释放时,电场力水平向右,因此绳子上作用力为零,故小球将沿合外力方向做匀变速直线运动,直至绳子被拉紧,根据数学关系可知恰好在最低点被拉紧.
(2)当小球从C点释放时,电场力水平向右,因此绳子上作用力为零,故小球将沿合外力方向做匀变速直线运动,直至绳子被拉紧,根据数学关系可知恰好在最低点被拉紧.
解答:解:(1)对小球由A到B的过程,由动能定理得:
mgL-EqL=0,故有:E=
.
故匀强电场的电场强度E的大小为:E=
.
(2)小球由C点释放后,将做匀加速直线运动,到B点速度大小为vb,设小球做匀加速直线运动的加速度为a,则:
a=
=
g
又:
=2a
L=4gL
得:t=
=
故小球到达最低点B所用的时间t=
.
mgL-EqL=0,故有:E=
| mg |
| q |
故匀强电场的电场强度E的大小为:E=
| mg |
| q |
(2)小球由C点释放后,将做匀加速直线运动,到B点速度大小为vb,设小球做匀加速直线运动的加速度为a,则:
a=
| ||
| m |
| 2 |
又:
| v | 2 b |
| 2 |
得:t=
| vb |
| a |
|
故小球到达最低点B所用的时间t=
|
点评:对于这类带点粒子在磁场中的运动问题一定要正确进形受力分析,弄清运动形式,然后选择适当规律求解.尤其注意功能关系与向心力公式的应用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 (2011?安徽二模)如图所示,在粗糙程度相同的斜面上固定一点电荷Q,在M点无初速度地释放带有恒定电荷的小物块,小物块在Q的电场中沿斜面运动到N点静止,则从M到N的过程中( )
(2011?安徽二模)如图所示,在粗糙程度相同的斜面上固定一点电荷Q,在M点无初速度地释放带有恒定电荷的小物块,小物块在Q的电场中沿斜面运动到N点静止,则从M到N的过程中( )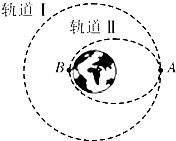 (2011?安徽二模)2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的是( )
(2011?安徽二模)2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道I进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的是( ) (2011?安徽二模)如图所示,以度v逆时针匀速转动的足够长的传送带与水平面的夹角为θ.现将一个质量为m的小木块轻轻地放在传送带的上端,小木块与传送带间的动摩擦因数为μ(μ<tanθ),则图中能够正确地描述小木块的速度随时间变化关系的图线是( )
(2011?安徽二模)如图所示,以度v逆时针匀速转动的足够长的传送带与水平面的夹角为θ.现将一个质量为m的小木块轻轻地放在传送带的上端,小木块与传送带间的动摩擦因数为μ(μ<tanθ),则图中能够正确地描述小木块的速度随时间变化关系的图线是( ) (2011?安徽二模)如图所示,水平轨道AB与半径为R的竖直半圆形轨道BC相切于B点.质量为2m和m的a、b两个小滑块(可视为质点)原来静止于水平轨道上,其中小滑块以与一轻弹簧相连.某一瞬间给小滑块以一冲量使其获得v0=3
(2011?安徽二模)如图所示,水平轨道AB与半径为R的竖直半圆形轨道BC相切于B点.质量为2m和m的a、b两个小滑块(可视为质点)原来静止于水平轨道上,其中小滑块以与一轻弹簧相连.某一瞬间给小滑块以一冲量使其获得v0=3 (2011?安徽二模)如图所示,斜面小车M静止在光滑水平面上,一边紧贴墙壁.若再在斜面上加一物体m,且M、m相对静止,此时小车受力个数为( )
(2011?安徽二模)如图所示,斜面小车M静止在光滑水平面上,一边紧贴墙壁.若再在斜面上加一物体m,且M、m相对静止,此时小车受力个数为( )