题目内容
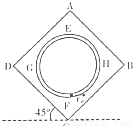
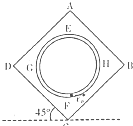 如图所示,在一匀强电场中,竖直面内有一正方形ABCD,CD边与水平面所成的角度为45°,CD边长为l=1m,电势φD=11V,φA=6V,φB=1V,ABCD内固定一个半径R=0.2m的光滑绝缘圆管,圆管的最上端、最下端=最左端和最右端分别为E、F、G、H,在圆管的底部有一质量m=1×10-6kg,电荷量为q=-
如图所示,在一匀强电场中,竖直面内有一正方形ABCD,CD边与水平面所成的角度为45°,CD边长为l=1m,电势φD=11V,φA=6V,φB=1V,ABCD内固定一个半径R=0.2m的光滑绝缘圆管,圆管的最上端、最下端=最左端和最右端分别为E、F、G、H,在圆管的底部有一质量m=1×10-6kg,电荷量为q=-| 2 |
| 0 | -6 |
| 3 |
分析:在匀强电场中沿电场线方向相等距离电势差相等,则知DB中点电势为6V,与A点电势相等,根据电场线与等势线垂直,可判断出电场线方向,由E=
求出场强的大小,计算出小球所受的电场力与重力大小,发现两者相等,等效的重力方向场沿BC方向,E点速度不是最小,轨迹EH的中点速度最小,根据动能定理求出小球达到EH中点的速度,与临界速度相比较,即可判断管壁对小球有无作用力.
| U |
| d |
解答:解:A、因为DB中点电势为6V,与A点电势相等,所以电场方向水平向右,E=
=5
V/m,故A错误.
B、小球所受的电场力大小F=qE=10-5N,重力大小G=mg=10-5N,则qE=mg,所以等效重力场沿BC方向,E点速度不是最小,轨迹EH的中点速度最小;故B错误.
C、D根据动能定理可算出EH中点的速度:-mg(R+
R)-qE
R=
m
-
m
,
=4(2-
),当管壁没有作用力时的速度为v,
mg=m
,v2=
gR=2
m/s,因为
<v2,所以里面的管壁对小球有作用力,故C错误,D正确.
故选D
| φB-φD | ||
|
| 2 |
B、小球所受的电场力大小F=qE=10-5N,重力大小G=mg=10-5N,则qE=mg,所以等效重力场沿BC方向,E点速度不是最小,轨迹EH的中点速度最小;故B错误.
C、D根据动能定理可算出EH中点的速度:-mg(R+
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| v | 2 min |
| 1 |
| 2 |
| v | 2 0 |
| v | 2 min |
| 2 |
| 2 |
| v2 |
| R |
| 2 |
| 2 |
| v | 2 min |
故选D
点评:本题突破口是根据D、A、B三点的电势关系,找到等势点,再确定出电场方向,运用E=
求出场强的大小.采用等效的方法判断小球速度最小的位置,由动能定理求速度,由牛顿第二定律求解临界速度.
| U |
| d |

练习册系列答案
相关题目
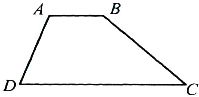 如图所示,在一匀强电场中有一梯形ABCD,其中AB∥CD,且AB=
如图所示,在一匀强电场中有一梯形ABCD,其中AB∥CD,且AB= 如图所示,在一匀强电场区域中,有A、B、C、D四点恰好位于一正方形的四个顶点上,已知A、B、C三点电势分别为φA=2V,φB=4V,φC=0.请在图中作出电场线(至少作两条),D点电势φD为
如图所示,在一匀强电场区域中,有A、B、C、D四点恰好位于一正方形的四个顶点上,已知A、B、C三点电势分别为φA=2V,φB=4V,φC=0.请在图中作出电场线(至少作两条),D点电势φD为
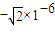 C的小球从F点以
C的小球从F点以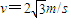 的速度在圆管内做完整的圆周运动小球的半径忽略不计,在运动过程中小球带电量不变.取g=10m/s2,以下说法正确的是( )
的速度在圆管内做完整的圆周运动小球的半径忽略不计,在运动过程中小球带电量不变.取g=10m/s2,以下说法正确的是( )