题目内容
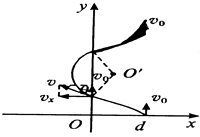
【题目】如图,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁感应强度B=0.5T,一带负电的粒子(比荷 ![]() =160C/kg),在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求:
=160C/kg),在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求: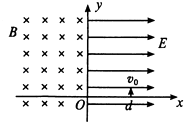
(1)带电粒子开始运动后第一次通过y轴的速度大小和方向;
(2)带电粒子进入磁场后经多长时间返回电场;
(3)带电粒子运动的周期.
【答案】
(1)解:粒子在第一象限做类平抛运动,
加速度a= ![]() =160×10=1600m/s2,
=160×10=1600m/s2,
由匀变速直线运动的位移公式得:x= ![]() at12,
at12,
代入数据解得:t1= ![]() s,
s,
沿y轴方向的位移:y=v0t1=8× ![]() =
= ![]() m,
m,
粒子通过y轴进入磁场时在x方向上的速度:vx=at1=1600× ![]() =8
=8 ![]() m/s,
m/s,
速度:v= ![]() ,代入数据解得:v=16m/s,
,代入数据解得:v=16m/s,
因此tanθ= ![]() =
= ![]() ,则:θ=60°;
,则:θ=60°;
答:带电粒子开始运动后第一次通过y轴的速度大小为:8 ![]() m/s,方向与y轴夹60°角;
m/s,方向与y轴夹60°角;
(2)解:粒子在第二象限以O′为圆心做匀速圆周运动,
圆弧所对的圆心角为2θ=120°,运动时间t2= ![]() T=
T= ![]() ×
× ![]() =
= ![]() =
= ![]() s;
s;
答:带电粒子进入磁场后经 ![]() s返回电场;
s返回电场;
(3)解:粒子从磁场返回电场后的运动是此前由电场进入磁场运动的逆运动,经时间t3=t1,
粒子的速度变为v0,此后得得前面的运动,可见,粒子在电、磁场中的运动具有周期性,
其周期:T=t1+t2+t3=( ![]() +
+ ![]() )s;
)s;
答:带电粒子运动的周期为( ![]() +
+ ![]() )s.
)s.
【解析】(1)由牛顿第二定律、运动学公式、运动的合成与分解可以求出粒子的速度;(2)粒子进入磁场后做匀速圆周运动,由几何关系可以确定粒子运动的圆心和半径;由转过的角度可以求出粒子在磁场中转动的时间;(3)粒子再回到初始状态所用的时间为一个周期,故周期包括两次电场中的运动和一次磁场中的运动,求得总时间即为一个周期.
【考点精析】利用洛伦兹力对题目进行判断即可得到答案,需要熟知洛伦兹力始终垂直于v的方向,所以洛伦兹力一定不做功.

 阅读快车系列答案
阅读快车系列答案