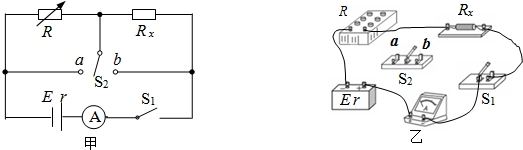
题目内容
如图甲所示,斜面与水平面间的夹角θ可以随意改变,可视为质点的小物块从斜面的底端以大小恒定的初速率v0沿斜面向上运动,所能上升的最大距离记为s.今改变θ而使s随之改变,根据所测量的若干组数据可以描述出“s-θ”曲线如图乙所示.若斜面足够长,取g=10m/s2,试根据“s-θ”曲线和相关的物理规律,分析求解: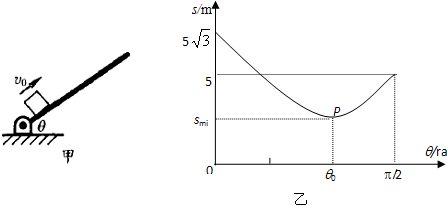
(1)从图中读出θ=
时物体运动的最大距离,并分析θ=
时物体的运动;
(2)小物块的初速率v0;
(3)小物块与斜面间的动摩擦因数?;
(4)对应“s-θ”曲线上s取最小值的P点的坐标值(θ0,smin)

(1)从图中读出θ=
| π |
| 2 |
| π |
| 2 |
(2)小物块的初速率v0;
(3)小物块与斜面间的动摩擦因数?;
(4)对应“s-θ”曲线上s取最小值的P点的坐标值(θ0,smin)
分析:(1)由图象可求出θ=
时,物体的运动最大距离,然后分析物体的运动情况;
(2)根据θ=
时物体的最大位移,应用匀变速运动的速度位移公式求出物体的初速度;
(3)由图象可知,当θ2=0时,x2=10m,当木板水平时,由动能定理得列出等式求解小木块与木板间的动摩擦系数.
(4)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理列出等式求解.
| π |
| 2 |
(2)根据θ=
| π |
| 2 |
(3)由图象可知,当θ2=0时,x2=10m,当木板水平时,由动能定理得列出等式求解小木块与木板间的动摩擦系数.
(4)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理列出等式求解.
解答:解:(1)由图象可知,当θ1=
时,x1=5m,此时物体做竖直上抛运动;
(2)当θ1=
时,x1=5m,物体做竖直上抛运动,
由速度位移公式公式可得:v02-0=2gx1,v0=
=
=10m/s;
(3)由图象可知,当θ2=0时,x2=5
m,此时木板水平,
由动能定理得:-μmgx2=0-
mv02,解得:μ=
;
(4)当板与水平方向夹角为θ时,沿斜面上滑的距离为s,由动能定理得:-mgssinθ-μmgscosθ=0-
mv02,
即s=
,
令a=sinθ+μcosθ=
(
sinθ-
cosθ),
设cosα=
,则a=
sin(α+θ),α+θ=
时,
a存在最大值,am=
=
,sinθ0=cosα=
=
=
,
θ0=arsin
,对应s的最小值为smin=
=
=
m;
P点的坐标值(arsin
,
).
答:(1)从图中读出θ=
时物体运动的最大距离为5m,θ=
时物体做竖直上抛运动;
(2)小物块的初速率为10m/s;
(3)小物块与斜面间的动摩擦因数为
;
(4)对应“s-θ”曲线上s取最小值的P点的坐标值(arsin
,
).
| π |
| 2 |
(2)当θ1=
| π |
| 2 |
由速度位移公式公式可得:v02-0=2gx1,v0=
| 2gx1 |
| 2×10×5 |
(3)由图象可知,当θ2=0时,x2=5
| 3 |
由动能定理得:-μmgx2=0-
| 1 |
| 2 |
| ||
| 3 |
(4)当板与水平方向夹角为θ时,沿斜面上滑的距离为s,由动能定理得:-mgssinθ-μmgscosθ=0-
| 1 |
| 2 |
即s=
| ||
| 2g(sinθ+μcosθ) |
令a=sinθ+μcosθ=
| 1+μ2 |
| 1 | ||
|
| μ | ||
|
设cosα=
| 1 | ||
|
| 1+μ2 |
| π |
| 2 |
a存在最大值,am=
1+(
|
2
| ||
| 3 |
| 1 | ||
|
| 1 | ||||||
|
| ||
| 2 |
θ0=arsin
| ||
| 2 |
| ||
| 2gam |
| 102 | ||||
2×10×
|
5
| ||
| 2 |
P点的坐标值(arsin
| ||
| 2 |
5
| ||
| 2 |
答:(1)从图中读出θ=
| π |
| 2 |
| π |
| 2 |
(2)小物块的初速率为10m/s;
(3)小物块与斜面间的动摩擦因数为
| ||
| 3 |
(4)对应“s-θ”曲线上s取最小值的P点的坐标值(arsin
| ||
| 2 |
5
| ||
| 2 |
点评:本题关键能够运用x-θ曲线的特殊值,选择物理规律解决问题.
了解研究对象的运动过程是解决问题的前提,选取研究过程,运用动能定理解题.
了解研究对象的运动过程是解决问题的前提,选取研究过程,运用动能定理解题.

练习册系列答案
相关题目
 在探究物体做平抛运动规律的实验中,某同学做了下图甲、乙所示的实验.如图甲所示的实验中,A、B两球同时落地,说明
在探究物体做平抛运动规律的实验中,某同学做了下图甲、乙所示的实验.如图甲所示的实验中,A、B两球同时落地,说明
 (2011?罗湖区模拟)某校研究性学习小组的同学用如图甲所示的滴水法测量一小车在斜面上运动时的加速度.实验过程如下:在斜面上铺上白纸,用图钉钉住;把滴水计时器固定在小车的末端;调节滴水计时器的滴水速度,使其每0.2s滴一滴(以滴水计时器内盛满水为准);在斜面顶端放置一浅盘,把小车放在斜面顶端,把调好的滴水计时器盛满水,使水滴能滴人浅盘内;随即在撤去浅盘的同时放开小车,于是水滴在白纸上留下标志小车运动规律的点迹;小车到达斜面底端时立即将小车移开.
(2011?罗湖区模拟)某校研究性学习小组的同学用如图甲所示的滴水法测量一小车在斜面上运动时的加速度.实验过程如下:在斜面上铺上白纸,用图钉钉住;把滴水计时器固定在小车的末端;调节滴水计时器的滴水速度,使其每0.2s滴一滴(以滴水计时器内盛满水为准);在斜面顶端放置一浅盘,把小车放在斜面顶端,把调好的滴水计时器盛满水,使水滴能滴人浅盘内;随即在撤去浅盘的同时放开小车,于是水滴在白纸上留下标志小车运动规律的点迹;小车到达斜面底端时立即将小车移开. 为了研究平抛物体的运动,可做下面的实验:如图甲所示,用小锤打击弹性金属片,B球就水平飞出,同时A球被松开,做自由落体运动,两球同时落到地面;如图乙所示的实验:将两个完全相同的斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是球1落到水平木板上击中球2,这两个实验说明( )
为了研究平抛物体的运动,可做下面的实验:如图甲所示,用小锤打击弹性金属片,B球就水平飞出,同时A球被松开,做自由落体运动,两球同时落到地面;如图乙所示的实验:将两个完全相同的斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是球1落到水平木板上击中球2,这两个实验说明( )