题目内容
11. 如图所示,在磁感应强度为B的磁场中,两导轨间距为L,某时刻两棒速度为v1和v2,且v1>v2,试由E=n$\frac{△Φ}{△t}$,求出此时回路中的感应电动势为多少?
如图所示,在磁感应强度为B的磁场中,两导轨间距为L,某时刻两棒速度为v1和v2,且v1>v2,试由E=n$\frac{△Φ}{△t}$,求出此时回路中的感应电动势为多少?
分析 振动两根导体棒的速度,由磁通量的计算式求出磁通量的变化,然后由法拉第电磁感应定律即可求出.
解答 解:(1)金属棒AB、CD都小于运动,且v1>v2,所以导体棒之间的面积上的磁通量增大,△Φ=B△S=BL(v1-v2)•△t
由法拉第电磁感应定律:E=$\frac{△Φ}{△t}$=$\frac{BL({v}_{1}-{v}_{2})△t}{△t}=BL({v}_{1}-{v}_{2})$
答:此时回路中的感应电动势为BL(v1-v2).
点评 本题中要求用E=n$\frac{△Φ}{△t}$计算电动势,由几何磁通量的计算公式即可求出.
另外,存在反电动势,两个动生电动势抵消后得到总电动势,根据公式E=BLv求出动生电动势的大小,由右手定则判断动生电动势的方向.根据电动势的方向,分析得出总电动势..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8Hz,乙弹簧振子的固有频率为7Hz,当支架受到竖直方向且频率为9Hz的驱动力作用做受迫振动时,则两个弹簧振子的振动情况是( )
如图两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8Hz,乙弹簧振子的固有频率为7Hz,当支架受到竖直方向且频率为9Hz的驱动力作用做受迫振动时,则两个弹簧振子的振动情况是( )
 如图两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8Hz,乙弹簧振子的固有频率为7Hz,当支架受到竖直方向且频率为9Hz的驱动力作用做受迫振动时,则两个弹簧振子的振动情况是( )
如图两个弹簧振子悬挂在同一支架上,已知甲弹簧振子的固有频率为8Hz,乙弹簧振子的固有频率为7Hz,当支架受到竖直方向且频率为9Hz的驱动力作用做受迫振动时,则两个弹簧振子的振动情况是( )| A. | 甲的振幅较大,且振动频率为8Hz | B. | 甲的振幅较大,且振动频率为9Hz | ||
| C. | 乙的振幅较大,且振动频率为9Hz | D. | 乙的振幅较大,且振动频率为7Hz |
2.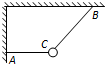 如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,其中不正确的是( )
如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,其中不正确的是( )
 如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,其中不正确的是( )
如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,其中不正确的是( )| A. | F1先变小后变大 | B. | F1先变大后变小 | C. | F2逐渐减小 | D. | F2最后减小到零 |
19.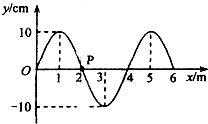 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=-10sin(5πt)cm.关于这列简谐波,下列说法正确的是( )| A. | 传播方向沿x轴正向 | B. | 周期为2.5s | ||
| C. | 传播速度为10m/s | D. | 经一个周期,质点P通过的路程为4m |
3.大小为1N、7N、9N的三个共点力作用在一个物体上,则( )
| A. | 三个力合力的最大值为17N | |
| B. | 三个力合力的最小值为零 | |
| C. | 三个力合力的最小值为1N | |
| D. | 三个力合力的方向不可能与其中某个力方向相同 |
 2014年3月8日凌晨2点40分,马来西亚航空公司一架载有239人的波音777-200飞机与管控中心失去联系.有关数据显示马航失联大约还能飞行5小时.假设航班在失联后仍处于正常匀速飞行状态,已知该飞机发动机的总功率约为8.25×104kw,受到的平均阻力约为3.3×105N,请你由此估算马航失联飞机在正常情况下还能飞行多远距离.
2014年3月8日凌晨2点40分,马来西亚航空公司一架载有239人的波音777-200飞机与管控中心失去联系.有关数据显示马航失联大约还能飞行5小时.假设航班在失联后仍处于正常匀速飞行状态,已知该飞机发动机的总功率约为8.25×104kw,受到的平均阻力约为3.3×105N,请你由此估算马航失联飞机在正常情况下还能飞行多远距离.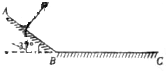 游乐园时有一种滑草的游乐活动,如图所示,人坐在滑板上从斜坡滑道上的A点由静止开始滑下,滑下斜坡滑道底部B点后沿水平滑道再滑行一段距离到C点停下来,斜坡滑道与水平滑道间是平滑连接的,滑板与两滑道间的动摩擦因数均为μ=0.4,不计空气阻力,重力加速度g=10m/s2.若人开始下滑位置的高度为h=36m,斜坡滑道倾角为37°,(已知sin37°=0.6,cos37°=0.8)
游乐园时有一种滑草的游乐活动,如图所示,人坐在滑板上从斜坡滑道上的A点由静止开始滑下,滑下斜坡滑道底部B点后沿水平滑道再滑行一段距离到C点停下来,斜坡滑道与水平滑道间是平滑连接的,滑板与两滑道间的动摩擦因数均为μ=0.4,不计空气阻力,重力加速度g=10m/s2.若人开始下滑位置的高度为h=36m,斜坡滑道倾角为37°,(已知sin37°=0.6,cos37°=0.8)