题目内容
2. 一质量为m的物体,放在倾角为30°的斜面上,恰能匀速下滑.
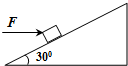
一质量为m的物体,放在倾角为30°的斜面上,恰能匀速下滑.(1)物体在大小为F的水平向右的恒力作用下,沿斜面匀速向上滑行,如图所示,当斜而倾角增大并超过某一值时,不论水平恒力F多大,都不能使物体沿斜而向上滑行,试求这一临界角的大小.
(2)保持斜面倾角30°不变,在竖直平面内施加外力,使物体沿斜面向上匀速滑行,求最小的外力大小和方向.
分析 (1)物体匀速下滑时受力平衡,根据共点力平衡条件并结合正交分解法列方程,同时结合摩擦力公式求解动摩擦因素μ,设斜面倾角为α,由匀速直线运动的条件求出推力的表达式,结合数学知识,即可求解临界角大小;
(2)设F与斜面成β角时,F最小,物体做匀速直线运动,受力平衡,根据平衡条件求出F的表达式,再结合数学方向求出最小的外力大小和方向.
解答 解:(1)恰能匀速下滑:mgsin30°=μmgcos30°
得:$μ=\frac{sin30°}{cos30°}=\frac{\sqrt{3}}{3}$
设斜面倾角为α,由匀速直线运动的条件:
沿斜面方向上有:Fcosα=mgsinα+f1
N1=mgcosα+Fsinα
f1=μN1
解得:$F=\frac{mgsinα+μmgcosα}{cosα-μsinα}$
当cosα-μsinα=0 即cotα=μ 时,F→∞,
即“不论水平恒力F多大,都不能使物体沿斜面向上滑行”此时,α=60°
(2)设F与斜面成β角时,F最小,物体做匀速直线运动,受力平衡,则有:
Fcosβ=mgsin30°+f2,
N2+Fsinβ=mgcos30°
f2=μN2
解得:F=$\frac{mgsin30°+μmgcos30°}{cosβ+μsinβ}$=$\frac{mg}{cosβ+μsinβ}$
当cosβ+μsinβ最大时,F最小,
对y=cosβ+μsinβ求导数,得:y′=μcosβ-sinβ
令y′=0得:tanβ=μ 即,β=30°时F最省,此时 F=$\frac{\sqrt{3}mg}{2}$
答:(1)这一临界角的大小为60°.
(2)最小的外力大小为$\frac{\sqrt{3}mg}{2}$,方向与斜面成30°斜向上.
点评 本题是简单的力平衡问题,关键是分析物体的受力情况,根据平衡条件列式求解,特别注意用数学知识来确定极值问题,难度较大.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案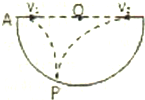 如图所示,半圆形凹槽的0点为其圆心.在与0点等高的边缘A、B两点分别以速度 V1、v2水平相向同时抛出两个小球,己知v1:v2=l:3,两小球恰落在弧面上的P点.则以下说法中正确的是( )
如图所示,半圆形凹槽的0点为其圆心.在与0点等高的边缘A、B两点分别以速度 V1、v2水平相向同时抛出两个小球,己知v1:v2=l:3,两小球恰落在弧面上的P点.则以下说法中正确的是( )| A. | ∠AOP为45° | |
| B. | A球先到达P点 | |
| C. | 若只增大Vl,两小球可在空中相遇 | |
| D. | 若要使两小球落在P点右侧的弧面上同一点,则应使Vl、v2都增大 |
 海南环岛自行车赛引人瞩目.下表是制造赛车各种材料的技术指标.
海南环岛自行车赛引人瞩目.下表是制造赛车各种材料的技术指标.| 材料技术指标 | 铬铝钢 | 铝合金 | 钛合金 | 碳纤维 |
| 性能(强度) | 强 | 较弱 | 较强 | 强 |
| 密度/(kg/m3) | 7.9×103 | 2.9×103 | 4.3×103 | 1.6×103 |
(1)若车架的体积约为3×10-3m3,则车架的最小质量是多大?
(2)若整车和赛车手的总重为700N,车轮与地面的总接触面积为10-3m2,请计算赛车手在比赛过程中对地面的压强.
(3)若赛车手在某路段匀速直线行驶,30s通过450m的路程,所受阻力约为60N,求赛车手匀速行驶的功率是多少?
(4)请说出赛车手在比赛过程中,用什么方法减小空气阻力提高成绩.(写出一种方法)

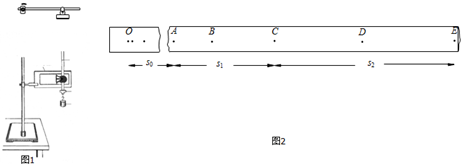
| A. | 整个过程中,CD段和DE段的加速度数值最大 | |
| B. | 整个过程中,BC段的加速度最大 | |
| C. | 整个过程中,D点离出发点最远 | |
| D. | 整个过程中,E点离出发点最远 |
| A. | 物体沿直线向某一方向运动,通过的路程就是位移 | |
| B. | 物体沿直线向某一方向运动,通过的路程等于位移的大小 | |
| C. | 物体通过一段路程,其位移可能是零 | |
| D. | 物体通过的路程不等,但位移可能相同,反之两物体通过的位移不同时,路程可能相同 |
 如图所示,轻杆的一端用铰链固定在竖直转轴OO′上的O端,另一端固定一小球,轻杆可在竖直平面内自由转动,当转轴以某一角速度匀速转动时,小球在水平面内做匀速圆周转动,此时轻杆与竖直转轴OO′的夹角为37°.已知转轴O端距离水平地面的高度为h,轻杆长度为L,小球的质量为m,重力加速度为g,取sin37°≈0.6,cos37°≈0.8,求:
如图所示,轻杆的一端用铰链固定在竖直转轴OO′上的O端,另一端固定一小球,轻杆可在竖直平面内自由转动,当转轴以某一角速度匀速转动时,小球在水平面内做匀速圆周转动,此时轻杆与竖直转轴OO′的夹角为37°.已知转轴O端距离水平地面的高度为h,轻杆长度为L,小球的质量为m,重力加速度为g,取sin37°≈0.6,cos37°≈0.8,求: 在如图所示,两条虚线之间区域内存在沿y轴负方向的匀强电场,场强大小为E,坐标系第四象限有一边长为$\sqrt{2}$L的绝缘正方形盒CDFG(内壁光滑),其内部存在垂直于纸面向外的匀强磁场(大小未知),且C、D两点恰好在x、y轴上,CD连线与x轴正方向成45°角.一质量为m,带电量为+q(重力不计)的带电粒子,从M板中心静止释放经MN两极板间的电场加速后,从N板中心孔S沿x轴正方向射入虚线区域内的电场中,经该电场偏转后垂直于CD从CD中点J处的小孔射入方盒内,已知粒子与盒壁碰撞过程中无动能和电荷损失.(所有结果只能用E、L、m、q表示)求:
在如图所示,两条虚线之间区域内存在沿y轴负方向的匀强电场,场强大小为E,坐标系第四象限有一边长为$\sqrt{2}$L的绝缘正方形盒CDFG(内壁光滑),其内部存在垂直于纸面向外的匀强磁场(大小未知),且C、D两点恰好在x、y轴上,CD连线与x轴正方向成45°角.一质量为m,带电量为+q(重力不计)的带电粒子,从M板中心静止释放经MN两极板间的电场加速后,从N板中心孔S沿x轴正方向射入虚线区域内的电场中,经该电场偏转后垂直于CD从CD中点J处的小孔射入方盒内,已知粒子与盒壁碰撞过程中无动能和电荷损失.(所有结果只能用E、L、m、q表示)求: