题目内容
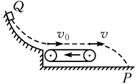
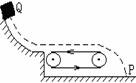
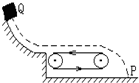 一物块m从某曲面上的Q点自由滑下,通过一粗糙的静止传送带后,落到地面P点(如图),若传送带的皮带轮沿逆时针方向转动起来,使传送带也随之运动,再把该物块放到Q点自由滑下,那它落在
一物块m从某曲面上的Q点自由滑下,通过一粗糙的静止传送带后,落到地面P点(如图),若传送带的皮带轮沿逆时针方向转动起来,使传送带也随之运动,再把该物块放到Q点自由滑下,那它落在P点
P点
(填:P点,P点左边,P点右边)分析:因传送带是逆时针转动,故不会对物体其带动作用,其做功仍是负功.无论传送带转动还是不转动,m滑过传送带所受摩擦力一样,经过的位移也一样,就是传送带两轮之间的长度,故两种情况下,传送带对物体做的功时一样的.由动能定理,可以知道两种情况下从传送带上抛出的速度关系,在由平抛规律可以得到落点位置.
解答:解:无论传送带静止,还是转动起来,物体m所受的都是滑动摩擦力,方向大小都一样,其次物体滑过传送带经过的位移就是传送带两轮之间的长度,故两次下滑在传送带上的位移也是一样的,故传送带对物体m做的功两次相等.又两次释放点相同,故两次重力做的功相同,故两次下滑力对物体做的总功相同.由动能定理,对从Q下滑到从传送带平抛出去:W=
mv2,可知两次平抛初速度相同,由平抛规律:x=v0t,h=
gt2,可知其水平和竖直位移都一样,故落地点也应一样,故仍在P点.
故答案为:P点
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:P点
点评:关键是要知道摩擦力力做的功一样的,这个与摩擦力的大小,和物体位移有关,能正确判定这两次,本题可解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目