��Ŀ����
9����ͼ1��ʾ��װ��BO��O������ֱ��OO��ת��������Ϊ�ʵ��С��A����ϸ�����Ӻ�ֱ�ϵ��B��C���㣬װ�þ�ֹʱϸ��ABˮƽ��ϸ��AC����ֱ����ļнǦ�=37�㣮����֪С�������m=1kg��ϸ��AC��L=1m��B���C���ˮƽ����ֱ������ȣ����������ٶ�gȡ10m/s2��sin37��=$\frac{3}{5}$��cos37��=$\frac{4}{5}$��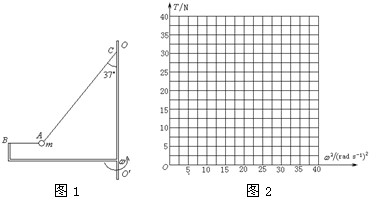
��1����װ������ת���Ľ��ٶ�Ϊ��1ʱ��ϸ��AB�ϵ�����Ϊ���ϸ��AC����ֱ����н���Ϊ37�㣬����ٶȦ�1�Ĵ�С��
��2����װ������ת���Ľ��ٶȦ�2=$\sqrt{\frac{50}{2}}$rad/s����ϸ��AC����ֱ����ļнǣ�
��3��װ�ÿ����Բ�ͬ�Ľ��ٶ�����ת������ͨ������������ͼ2�л���ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵͼ��
���� ��1��ϸ��AB������ǡΪ��ʱС�������������ĺ����ṩ������������ţ�ٵڶ�����������ٶȵĴ�С��
��2��${��_{2}}=\sqrt{\frac{50}{3}}{rad/s}$��${��_{1}}=\sqrt{\frac{50}{4}}{rad/s}$ʱ��ϸ��AB�ɳڣ�����С�������������ĺ����ṩ���������ϸ��AC����ֱ����ļнǣ�
��3������ţ�ٵڶ����ɷֱ����$�ء�{��_{1}}=\frac{5}{2}\sqrt{2}{rad/s}$ʱ����1�ܦءܦ�2ʱ���أ���2ʱ�����Ĵ�С���Ӷ�ȷ��ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵ��������ͼ��
��� �⣺��1����ϸ��AB�ϵ�����Ϊ���ϸ��AC����ֱ����н���Ϊ37��ʱ����װ������ת���Ľ��ٶ�Ϊ��1��С��������ͼ��ʾ��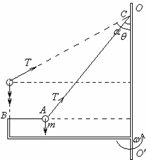
����mgtan��=$m��_1^2Lsin��$
�æ�1=$\sqrt{\frac{g}{Lcos��}}$=$\sqrt{\frac{50}{4}}$rad/s=$\frac{{5\sqrt{2}}}{2}$rad/s
��2����װ��ת�����ٶȱ��С�����ƣ�ϸ������ֱ����нDZ��ֱ��BAϸ����ֱ���ɼ��ι�ϵ��֪��Ӧƫ�Ǧ�=53�㣮���ʱϸ��AB����Ϊ��ʱ��Ӧ���ٶ�Ϊ��0������mgtan��=$m��_0^2Lsin��$�æ�0=$\sqrt{\frac{50}{3}}$rad/s
���ڦ�2=$\sqrt{\frac{50}{2}}$rad/s��$\sqrt{\frac{50}{3}}$rad/s������ϸ��AC����ֱ����ļн�Ϊ��=53�㣮
��3���ءܦ�1ʱ��ϸ��AC������ˮƽ�����ṩ����������ֱ������С������ƽ�⣬��Tcos��=mg��T=$\frac{50}{4}$N��1�ܦءܦ�0ʱ��ϸ��AB�ɳڣ�ϸ��AC������ˮƽ�����ṩ����������Tsinϕ=m��2Lsinϕ����T=m��2L�أ���0ʱ��ϸ��AB��С�������µ������ã�������Ȼ��ϸ��AC������ˮƽ�����ṩ����������Tsin��=m��2Lsin����
��T=m��2L
�����������ءܦ�1ʱ��T=$\frac{50}{4}$N=12.5N����أ���1ʱ��T=m��2L=��2
���ԣ�ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵͼ����ͼ��ʾ��
�𣺣�1�����ٶȦ�1�Ĵ�СΪ$\frac{5\sqrt{2}}{2}rad/s$��
��2��ϸ��AC����ֱ����ļн�Ϊ53�㣮
��3��ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵͼ����ͼ��
���� �������Ĺؼ�����С����Բ���˶�����������Դ��ȷ��С���˶������е��ٽ�״̬������ţ�ٵڶ����ɽ�����⣮

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| A�� | ���Ʀ�A����B����ǿEA��EB | |
| B�� | ���Ʀ�A����B����ǿEA��EB | |
| C�� | ��+q��ɴ�A���ƶ���B��糡�������� | |
| D�� | ��-q��ɷֱ����A��B����ʱ���еĵ�����EPA��EPB |
| A�� | $\frac{{d{v_2}}}{{\sqrt{v_2^2-v_1^2}}}$ | B�� | $\frac{{d{v_1}}}{v_2}$ | C�� | 0 | D�� | $\frac{{d{v_2}}}{v_1}$ |
| A�� | FN����Ff��С | B�� | Ff����FN��С | C�� | FN��Ff�������� | D�� | FN��Ff����С |
| A�� | ���������� | B�� | ������ | C�� | ������ | D�� | �׳�� |
 ����������ȣ��ֱ�������硢����Ͳ�����Ŀ�������ˮƽ���õ�ƽ�д���������������ͬ�ٶ�V0��ֱ�糡�߷���������ǿ�糡���ֱ����ڴ�����ɵ��°��ϵ�a��b��c���㣬��ͼ��ʾ�������ж���ȷ���ǣ�������
����������ȣ��ֱ�������硢����Ͳ�����Ŀ�������ˮƽ���õ�ƽ�д���������������ͬ�ٶ�V0��ֱ�糡�߷���������ǿ�糡���ֱ����ڴ�����ɵ��°��ϵ�a��b��c���㣬��ͼ��ʾ�������ж���ȷ���ǣ�������| A�� | ����a��Ŀ��������硢C��Ĵ����硢b��IJ����� | |
| B�� | ����a��b��c������ڵ糡�еļ��ٶȵĹ�ϵ��aa��ab��ac | |
| C�� | ���������˶���������ʱa�����Ķ������b����������С | |
| D�� | �糡��������b��Ŀ��������� |
 ���о�С����ƽ���˶����ɵ�ʵ���У�����õ�ʵ�����ݾ������������õ���ͼ��ʾ��y-x2ͼ������y��ʾС�����ֱλ�ƣ�x��ʾС���ˮƽλ�ƣ����ƿ���������ȡg=9.8m/s2����С����ƽ���˶��ij��ٶȴ�СΪ��������
���о�С����ƽ���˶����ɵ�ʵ���У�����õ�ʵ�����ݾ������������õ���ͼ��ʾ��y-x2ͼ������y��ʾС�����ֱλ�ƣ�x��ʾС���ˮƽλ�ƣ����ƿ���������ȡg=9.8m/s2����С����ƽ���˶��ij��ٶȴ�СΪ��������| A�� | 1m/s | B�� | $\sqrt{4.9}$m/s | C�� | 2m/s | D�� | 4.9m/s |
 ����ʱ�����õ�Դ��Ƶ��Ϊ50Hz��ij��ʵ���еõ���һ��ֽ�����ú��̶ȳ߲��������ͼ��ֽ����A��C��ʱ��0.04s��A��C��λ��1.40 cm��A��C���ƽ���ٶ�Ϊ0.35m/s����A��D���ƽ���ٶ�Ϊ0.42m/s��B���˲ʱ�ٶȸ��ӽ���0.35m/s�����������С�������λ��
����ʱ�����õ�Դ��Ƶ��Ϊ50Hz��ij��ʵ���еõ���һ��ֽ�����ú��̶ȳ߲��������ͼ��ֽ����A��C��ʱ��0.04s��A��C��λ��1.40 cm��A��C���ƽ���ٶ�Ϊ0.35m/s����A��D���ƽ���ٶ�Ϊ0.42m/s��B���˲ʱ�ٶȸ��ӽ���0.35m/s�����������С�������λ��