Question

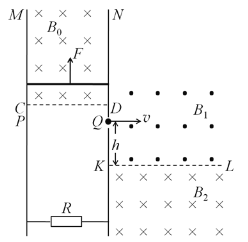
【题目】如图，竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N，两板间接一阻值R=2Ω的电阻，N板上有一小孔Q，在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场，N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场，磁感应强度大小分别为B1=3T和B2=2T。有一质量M=0.2kg、电阻r=1Ω的金属棒搭在MN之间并与MN良好接触，用输出功率恒定的电动机拉着金属棒竖直向上运动，当金属棒达最大速度时，在与Q等高并靠近M板的P点静止释放一个比荷1×104C/kg的正离子，经电场加速后，以v=200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力，忽略电流产生的磁场，取g=10m/s2。求：

（1）金属棒达最大速度时，电阻R两端电压U；

（2）电动机的输出功率P；

（3）离子从Q点进入右侧磁场后恰好不会回到N板，Q点距分界线高h等于多少？

Answer 1

【答案】（1）2V（2）9W（3）1.2×10-2m

【解析】

考查带电粒子在复合场中的运动。

（1）离子从P运动到Q，由动能定理：

解得R两端电压U=2V；

（2）感应电动势为：

由闭合电路欧姆定律：

电流：

安培力：

金属棒受力平衡：

功率：

联立解得电动机功率P=9W；

（3）如图所示，设离子恰好不会回到N板时，对应的离子在上下区域运动半径分别为r1和r2，圆心连线与N板夹角为φ。

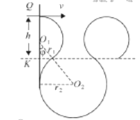
在磁场中，有：

解得，

几何关系：

解得h=1.2×10-2m。