题目内容
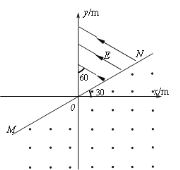
【题目】如图所示,板长和板间距均为2d的平行金属薄板M、N竖直放置,板间存在水平向左的匀强电场,场强始终不变,OO′为中轴线.O′为中轴线与PQ边界的交点.在板的正下方距离d处存在垂直纸面向里的匀强磁场,PQ是磁场的水平上边界,磁场足够宽.在板的正上方有一发射装置,在宽度为2d的范围内竖直向下发射出一束具有相同质量m、电荷量q的正电粒子(不计重力和粒子之间的相互作用),速度均为v0.已知紧贴N板入射的某粒子射出电场时恰好经过中轴线.求:
(1)电场强度E的大小;
(2)使该粒子恰好能从O′点射出磁场,磁感应强度应取何值;
(3)磁感应强度取何值,能使所有进入磁场的粒子偏转后均不能击中N板的下端.

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1) 该粒子在电场中做类平抛运动,由平抛运动规律有:
![]()
![]()
根据牛顿第二定律得:Eq=ma
联立解得:![]() ;
;
(2) 该粒子水平方向的分速度:
![]()
解得:![]()
根据勾股定理得,粒子进入磁场的速度大小:
![]()
方向斜朝左下方与竖直方向成45°角
该粒子在磁场中作圆周运动,洛仑兹力提供向心力有:
![]()
如图,轨迹①
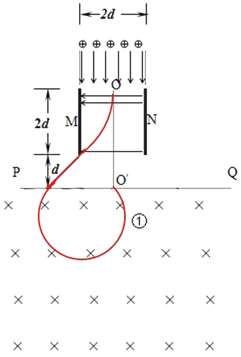
由几何关系:![]()
解得:![]() ;
;
(3) 依题意,进入磁场的所有粒子的运动规律都相同
ⅰ从板中央射出的粒子恰好能击中N板下端的轨迹②如图

由几何关系可知
![]()
解得:![]()
ⅱ紧贴M板下边缘射出的粒子恰好能击中N板下端的轨迹③如图
由几何关系可知
![]()
解得:![]()
所求范围:![]() 或
或![]() 。
。

练习册系列答案
相关题目