题目内容
质量为M的小车静止在光滑的水平面上,小车的上表面是一光滑的曲面,末端是水平的,如图1-8-12所示.小车被挡板P挡住,质量为m的物体从距地面高H处自由下落,然后沿光滑的曲面继续下滑,物体落地点与小车右端距离为s0.若撤去挡板P,物体仍从原处自由落下,求物体落地时落地点与小车右端距离是多少?
图1-8-12
解析:当小车被挡住时,物体落在小车上沿曲面向下滑动,对小车有斜向下方的压力,由于P的作用小车处于静止状态,物体离开小车时速度为v1,最终平抛落地.当去掉挡板,由于物对车的作用,小车将向左加速运动,动能增大,物体相对车滑动的同时,随车一起向左移动,整个过程机械能守恒,物体滑离小车时的动能将比在前一种情况下小,最终平抛落地.小车同时向前运动,所求距离是物体平抛过程中的水平位移与小车位移的和.求出此种情况下物体离开车时的速度v2,及此时车的速度v2′以及相应运动的时间是关键.在物体与小车相互作用过程中水平方向动量守恒,这是解决v2、v2′间关系的具体方法.
(1)挡住小车时,求物体滑落时的速度v1,物体从最高点下落至滑离小车时机械能守恒,设车尾部(右端)离地面高为h,则有
mg(H-h)=![]() mv12 ①
mv12 ①
由平抛运动的规律s0=v1t ②
h=![]() gt2. ③
gt2. ③
(2)设去掉挡板时物体离开小车时速度为v2,小车速度为v2′,物体从最高点至离开小车之时系统机械能守恒
mg(H-h)=![]() mv22+
mv22+![]() Mv2′2 ④
Mv2′2 ④
物体与小车相互作用过程中水平方向动量守恒Mv2′-mv2=0 ⑤
此式不仅给出了v2与v2′的大小关系,同时也说明了v2是向右的.
物体离开车后对地平抛s2=v2t′ ⑥
h=![]() gt′2 ⑦
gt′2 ⑦
车在t′时间内向前的位移s2′=v2′t′ ⑧
比较式⑦③得t′=t
解式①④⑤得v2=![]() v1,v2′=
v1,v2′=![]() v2.
v2.
此种情况下落地点距车右端的距离
s=s2+s2′=(v2+v2′)t=(1+![]() )v2t=
)v2t=![]() v1t=s0
v1t=s0![]() .
.
答案:s=s0![]()


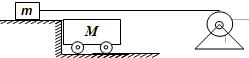 如图所示,质量为M的小车静止在光滑的水平面上,质量为m的小滑块在电动机的牵引下以恒定的速度向前运动,现使小滑块滑到小车上,经过一段时间后,m与M处于相对静止,从小滑块滑到小车到与小车相对静止的整个过程中小滑块的速度始终保持为v不变,它与小车之间的动摩擦因数为μ,求:
如图所示,质量为M的小车静止在光滑的水平面上,质量为m的小滑块在电动机的牵引下以恒定的速度向前运动,现使小滑块滑到小车上,经过一段时间后,m与M处于相对静止,从小滑块滑到小车到与小车相对静止的整个过程中小滑块的速度始终保持为v不变,它与小车之间的动摩擦因数为μ,求: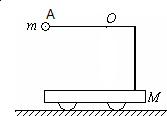 质量为M的小车静止在光滑的水平面上,质量为m的小球用细绳吊在小车上O点,将小球拉至水平位置A点静止开始释放(如图所示),其中OA的长为L,则小球落至最低点时相对地的速度
质量为M的小车静止在光滑的水平面上,质量为m的小球用细绳吊在小车上O点,将小球拉至水平位置A点静止开始释放(如图所示),其中OA的长为L,则小球落至最低点时相对地的速度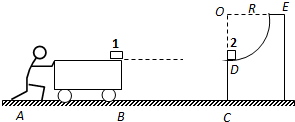 如图所示,一辆质量为M的小车静止在水平面上,车面上右端点有一可视为质点的滑块1,水平面上有与车右端相距为4R的固定的
如图所示,一辆质量为M的小车静止在水平面上,车面上右端点有一可视为质点的滑块1,水平面上有与车右端相距为4R的固定的