��Ŀ����
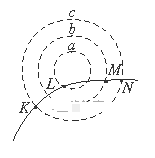
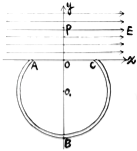
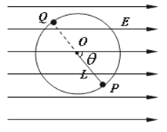
����Ŀ����ͼ��ʾ������ֱƽ���ڣ��ó�ΪL�ľ�Ե����������Ϊm��������Ϊ+q��С������O�㣬����װ�ô���ˮƽ���ҵ���ǿ�糡�С���ʼʱ��С��ֹ��P�㡣ϸ���볡ǿ����ɽǡ����þ�Ե��������ֱƽ�桢��ֱ��OP������һ��С��֮��Ѹ�ٳ��봸�ӣ���С��ص�P��ʱ���ٴ��ô�����ͬһ������С�����δ����С��ǡ�õ���Q�㣬��С������Բ���˶��������ʱ�伫�̣�С����������ʧ�����ӵ�һ�ζ�С������ΪW1���ڶ��ζ�������ΪW2��
��1������ǿ�糡�ij�ǿ��СE��
��2����![]() ��ֵ�ﵽ��ֱ���W1��W2;
��ֵ�ﵽ��ֱ���W1��W2;
���𰸡���1��![]() ����2��
����2��![]() ��
��![]()
��������
(1)С����ͼ��P�����Ϊ�㣬���У�tan��=![]()
��ã�E=![]() ��
��
(2)��Ч����FΪ����mg��糡��qE�ĺ�����������OP����![]()
Ϊʹ![]() �����ʹW1���W2��С����ϸ�������ɳڣ����Դ��ӵ�һ�δ��С���ǡ����ʹϸ��ת��90������������´��Ӷ�С������ΪW1��
�����ʹW1���W2��С����ϸ�������ɳڣ����Դ��ӵ�һ�δ��С���ǡ����ʹϸ��ת��90������������´��Ӷ�С������ΪW1��
���ݶ��ܶ����У�![]()
���:![]()
���ӵڶ��ζ�С������ʹС���P���˶���Q�㣬��Q�㣬С��ĵ�Ч����F�պ��ṩ����������������´��ӵڶ��ζ�С������ΪW2
��Q�㣬![]()
��ã�![]()
���ݶ��ܶ����У�![]()
��ã�![]()

��ϰ��ϵ�д�
�����Ŀ