题目内容
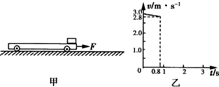 某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v0=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求:
某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v0=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求:
(1)小车的质量及车与地面的动摩擦因数;
(2)当小车停止时,车上有多少块砖?
解:(1)小车的上表面光滑,砖块相对地面始终保持静止状态,放上砖块后小车开始做匀减速运动,设小车与地面间的动摩擦因数为μ,则μMg=F
放上第一块砖后,对小车
F-μ(m+M)g=Ma1
即-μmg=Ma1
由v-t图象可知,△v1=v1-v0=2.8-3.0(m/s)=-0.2m/s,放第一块砖后小车的加速度为
解得,μ=0.25,M=8kg
(2)同理,放第二块砖后,对小车有
-2μmg=Ma2,
0.8s内速度改变:△v2=a2T=-0.4m/s
放第三块砖后小车的加速度为a3=-3×0.25m/s2=-0.75m/s2
0.8s内速度改变:△v3=-3×0.2m/s=-0.6m/s
则放第n块砖后小车的加速度: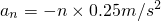 (n=1,2,3…)
(n=1,2,3…)
0.8s内速度改变:△vn=-n×0.2m/s(n=1,2,3…)
所以△v=△v1+△v2+△v3+…+△vn=-(1+2+3…+n)×0.2m/s
而△v=0-3m/s=-3m/s
联立解得,n=5
即当小车停止时,车上有5块砖.
答:
(1)小车的质量为8kg,车与地面的动摩擦因数为0.25;
(2)当小车停止时,车上有5块砖.
分析:(1)据题,小车的上表面光滑,砖块放到小车上后水平不受外力,相对地面始终保持静止状态.小车原来匀速前进,放上砖块后小车开始做匀减速运动,根据牛顿第二定律得出小车的加速度与动摩擦因数的关系,由v-t图象斜率大小求出加速度,联立求解小车的质量及车与地面的动摩擦因数.
(2)根据牛顿第二定律分别求出放上第二块砖、第三块砖、…小车的加速度,由速度公式求出每一个0.8s内小车速度的改变量,总结规律,得出放上第n块砖后0.8s内小车的速度改变量,得出小车速度减至零时改变量的表达式,求出当小车停止时,车上有多少块砖.
点评:本题分析受力情况和运动情况是基础,难点是运用数学归纳法总结规律,得出小车速度改变量的通项.
放上第一块砖后,对小车
F-μ(m+M)g=Ma1
即-μmg=Ma1
由v-t图象可知,△v1=v1-v0=2.8-3.0(m/s)=-0.2m/s,放第一块砖后小车的加速度为

解得,μ=0.25,M=8kg
(2)同理,放第二块砖后,对小车有
-2μmg=Ma2,

0.8s内速度改变:△v2=a2T=-0.4m/s
放第三块砖后小车的加速度为a3=-3×0.25m/s2=-0.75m/s2
0.8s内速度改变:△v3=-3×0.2m/s=-0.6m/s
则放第n块砖后小车的加速度:
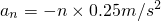 (n=1,2,3…)
(n=1,2,3…)0.8s内速度改变:△vn=-n×0.2m/s(n=1,2,3…)
所以△v=△v1+△v2+△v3+…+△vn=-(1+2+3…+n)×0.2m/s
而△v=0-3m/s=-3m/s
联立解得,n=5
即当小车停止时,车上有5块砖.
答:
(1)小车的质量为8kg,车与地面的动摩擦因数为0.25;
(2)当小车停止时,车上有5块砖.
分析:(1)据题,小车的上表面光滑,砖块放到小车上后水平不受外力,相对地面始终保持静止状态.小车原来匀速前进,放上砖块后小车开始做匀减速运动,根据牛顿第二定律得出小车的加速度与动摩擦因数的关系,由v-t图象斜率大小求出加速度,联立求解小车的质量及车与地面的动摩擦因数.
(2)根据牛顿第二定律分别求出放上第二块砖、第三块砖、…小车的加速度,由速度公式求出每一个0.8s内小车速度的改变量,总结规律,得出放上第n块砖后0.8s内小车的速度改变量,得出小车速度减至零时改变量的表达式,求出当小车停止时,车上有多少块砖.
点评:本题分析受力情况和运动情况是基础,难点是运用数学归纳法总结规律,得出小车速度改变量的通项.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
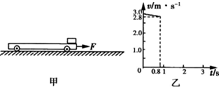 某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v0=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求:
某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v0=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求: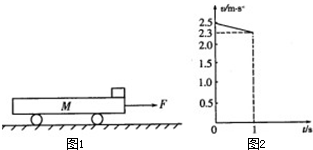
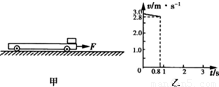 某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求:
某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求: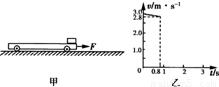 某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求:
某电视台在游乐园举行家庭搬运砖块比赛活动,比赛规则是向沿水平面做直线运动的小车上搬放砖块,每次只能将一块砖无初速(相对于地面)地放到车上,车停止时立即停止搬运,以车上砖块多少决定胜负.已知小车的上表面光滑且足够长,且小车与地面的动摩擦因数不变,比赛过程中车始终受到水平恒定的牵引力F=20N的作用,未放砖块时车以v=3.0m/s匀速前进.某家庭上场比赛时每隔T=0.8s搬放一块砖;已知每块砖的质量m=0.8kg,从放上第一块砖开始计时,图2中仅画出了0~0.8s内车运动的v-t图象,整个过程中砖始终在车上未滑下,取g=10m/s2,求: