题目内容
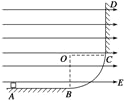
【题目】实验中经常利用电磁场来改变带电粒子运动的轨迹。如图所示,氕、氘、氚三种粒子同时沿直线在纸面内通过电场强度为E、磁感应强度为B的复合场区域。进入时氕与氘、氘与氚的间距均为d,射出复合场后进入y轴与MN之间(其夹角为θ)垂直于纸面向外的匀强磁场区域Ⅰ,然后均垂直于边界MN射出。虚线MN与PQ间为真空区域Ⅱ且PQ与MN平行。已知质子比荷为![]() ,不计重力。
,不计重力。
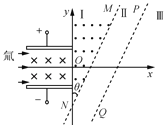
(1)求粒子做直线运动时的速度大小v;
(2)求区域Ⅰ内磁场的磁感应强度B1;
(3)若虚线PQ右侧还存在一垂直于纸面的匀强磁场区域Ⅲ,经该磁场作用后三种粒子均能汇聚于MN上的一点,求该磁场的最小面积S和同时进入复合场的氕、氚运动到汇聚点的时间差△t。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
由电场力与洛伦兹力平衡即可求出速度;由洛伦兹力提供向心力结合几何关系即可求得区域Ⅰ内磁场的磁感应强度B1;分析可得氚粒子圆周运动直径为3r,求出磁场最小面积,在结合周期公式即可求得时间差。
(1)粒子运动轨迹如图所示:
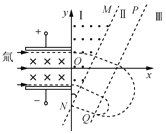
由电场力与洛伦兹力平衡,有:Bqv=Eq
解得:![]()
(2)由洛伦兹力提供向心力,有:![]()
由几何关系得:r=d
解得:![]()
(3)分析可得氚粒子圆周运动直径为3r,磁场最小面积为:![]()
解得:S=πd2
由题意得:B2=2B1
由![]() 可得:
可得:![]()
由轨迹可知:△t1=(3T1﹣T1)![]() ,
,
其中![]()
△t2=![]() (3T2﹣T2)其中
(3T2﹣T2)其中![]()
解得:△t=△t1+△t2=![]()

练习册系列答案
相关题目