题目内容
【题目】滑板运动是时下许多年轻人所热爱的极限运动项目,图示为一段水平粗糙平台AB和光滑半圆轨道组成的表演场地,某运动员在平台AB段通过蹬地获得水平推力,加速滑至B点后平抛落于圆周轨道上的C处,圆轨道最低处装有力传感器,可显示运动员通过时对轨道的压力大小,已知:平台动摩擦因数μ=0.2,长度LAB=5m,运动员(含滑板)质量m=60kg,AB段获得的平均推力F=360N,C处距平台平面的竖直高度h=2m,求:
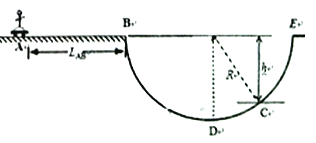
(1)运动员到达B点处的速度大小;
(2)该圆轨道的半径R的大小;
(3)若传感器显示压力F压=2200N,运动员在C处于轨道碰撞损失的机械能![]()
【答案】(1)![]() (2)2.5m(3)700J
(2)2.5m(3)700J
【解析】(1)在AB段,对运动员受力分析,根据牛顿第二定律,有:F-μmg=ma
代入数据解得:a=4m/s2
由匀变速直线运动速度与位移关系式有:vB20=2aLAB
得:vB=2![]() m/s
m/s
(2)由平抛运动的规律有:h=![]() gt2
gt2
可得:![]()
x=vBt=2![]() ×
×![]() m=4m
m=4m
由几何规律得:(R-x)2+h2=R2
代入数据解得:R=2.5m
(3)由题意可知:F'=F压=2200N
在D点,对运动员有:F′mg=m![]()
C→D过程中,由动能定理有:mg(R-h)=EkD-EkC
解得:EkC=![]() mvD2mg(Rh)
mvD2mg(Rh)
所以 △E=![]() mvB2+mghEKC=700J
mvB2+mghEKC=700J

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目