��Ŀ����
����Ŀ����ͼ��ʾ��һ����������Ϊm=2.0��10��11kg�������q=+1.0��10��5C���Ӿ�ֹ��ʼ����ѹΪU1=100V�ĵ糡���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У�������糡ʱ��ƫת�Ǧ�=30�㣬�����Ž���һ������ֱֽ���������ΪD=34.6cm����ǿ�ų�������֪ƫת�糡�н����峤L=20cm��������d=17.3cm���������Բ��ƣ���
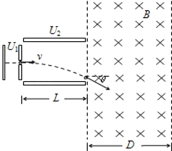
��1������������ƫת�糡ʱ������v1��
��2��ƫת�糡�����������ĵ�ѹU2��
��3��Ϊʹ�����������ɴų��ұ����������ǿ�ų��ĴŸ�Ӧǿ��B���ٶ��١�
���𰸡�(1)1.0��104m/s (2)100 V (3)0.1 T
��������
��1�������ڼ��ٵ糡�У��糡���������ɶ��ܶ�������ٶ�v1��
��2�����ӽ���ƫת�糡������ƽ���˶��������˶��ĺϳ���ֽ������ѹ��
��3�����ӽ���ų���������Բ���˶�����������������켣���ɼ���֪ʶ��뾶������B��
��1�������������ٵ糡���ٺ��ٶ�Ϊv�����ݶ��ܶ�����qU1��![]() mv12
mv12
��ã�v1��![]() =1.0��104m/s
=1.0��104m/s
��2����������ƫת�糡��ֻ�ܵ糡�����ã�����ƽ���˶�����ˮƽ������������ֱ���˶�ˮƽ����![]()
����������ֱ�������ȼ���ֱ���˶������ٶ�Ϊa�����糡ʱ��ֱ�����ٶ�Ϊv2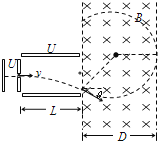
��ֱ����![]()
v2��at��![]()
�ɼ��ι�ϵ��![]()
U2��![]() tan��
tan��
�������ݵã�U2=100V
��3������������ų�������Բ���˶������������ṩ����������������뾶ΪR���ɼ��ι�ϵ֪R+![]() ��D
��D
�ã�R��![]()
��������ų�ʱ���ٶ�Ϊv����v����![]()
��ţ���˶����ɼ��˶�ѧ���ɣ�qv��B��![]()
�ã�![]()
�����������ݽ��B=0.1T
���������Ӳ�����ų����Ÿ�Ӧǿ��B����Ϊ0.1T��

 ͨ��ѧ��Ĭд����ϵ�д�
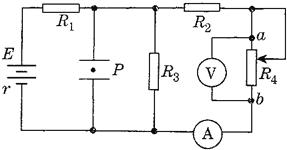
ͨ��ѧ��Ĭд����ϵ�д�����Ŀ��һͬѧ����ͼ��ʾװ���о���Ӧ���������������Ӧ�����Ĵų��仯�Ĺ�ϵ����֪�����ӽ�����a���������ʱ��������ָ����ƫ��ʵ��ʱԭ�ų��������˶������������ָ�����¼���±���
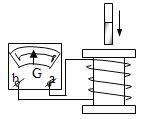
ʵ����� | �����Ӧ�����Ĵų����� | �����˶���� | ָ��ƫת��� |
1 | ���� | ���� | ��ƫ |
2 | ���� | �γ� | ��ƫ |
3 | ���� | ���� | ��ƫ |
4 | ���� | �γ� | ��ƫ |
��1����ʵ��1��3�ó��Ľ����ǣ������պϻ�·�Ĵ�ͨ��_____������ӡ��������١���ʱ����Ӧ�����Ĵų������������Ӧ�����Ĵų�����________�����ͬ�������෴������
��2����ʵ��2��4�ó��Ľ����ǣ������պϻ�·�Ĵ�ͨ�� ______������ӡ��������١���ʱ����Ӧ�����Ĵų������������Ӧ�����Ĵų����� ________�����ͬ�������෴������
��3����ʵ��1��2��3��4�ó��Ľ����ǣ�________________________________________.